52.
Интервальные оценки
и генеральной дисперсии, которые проводились одним числом. Такие оценки называются точечными. Часто бывает необходимо не просто оценить некоторый параметр генеральной совокупности одним числом, но еще и указать интервал, в который этот параметр попадает с заданной вероятностью. Оценки, которые определяются двумя числами — концами интервала — называют интервальными.Будем для определенности говорить об интервальной оценке генерального среднего, хотя рассматривают также оценки генеральной дисперсии, вероятности и т.п. Пусть 
— это неизвестное генеральное среднее, которую оценивают при помощи выборочного среднего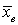 
. Ес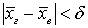ли 
(или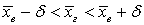 
), то говорят, что интервал шириной 2 δ покрывает неизвестное истинное значение группового среднего . Положительное число δ характеризует точность оценки: чем меньше δ, тем точность оценки выше. Интервал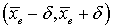 
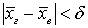называется доверительным интервалом. Выборочное среднее, а, значит, и границы интервала являются случайными величинами, поэтому можно говорить лишь о некоторой вероятности, что интервал покрывает неизвестное значение . Вероятность, что называют надежностью (или доверительной вероятностью) и будем обозначать ее символом γ. Обычно требуемую надежность задают числами 0,95, 0,99 или 0,999 и находят интервал δ в окрестности 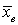, который покрывает неизвестное с этой вероятностью. Более точно, с математической точки зрения: нужно найти такую δ, что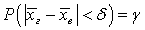 
.Чтобы посчитать вероятность, нужно сделать некоторые предположения о распределении рассматриваемого признака в генеральной совокупности. Будем считать, что случайная величина — значения рассматриваемого признака — имеет нормальное распределение 
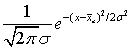с известным среднеквадратичным отклонением σ. Такое предположение вполне может быть оправдано центральной предельной теоремой, рассмотренной в кванте 43. Если случайная величина распределена нормально, то и выборочное среднее имеет нормальное распределение с тем же математическим ожиданием, но другим среднеквадратичным отклонением, а именно: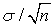 
. Тогда 
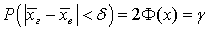, где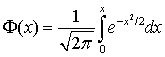 
— функция Лапласа, а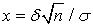 
. Здесь для получения вероятности было проинтегрировано нормальное распределение в пределах δ-окрестности от пика распределения (2 Ф (x)) и учтена четность подынтегрального выражения.Резюмируя, для получения доверительного интервала поступают следующим образом. Задается надежность γ. Далее, используя таблицу (см. квант 22) или какой-либо вычислительный пакет, работающий с функцией Лапласа
(или интегралом ошибок), из соотношения 2 Ф (x) = γ определяют x. В частности, для γ, равных 0,95, 0,99 и 0,999, имеем: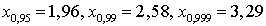
.Далее по найденному вычисляется доверительный интервал:
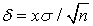.Этот интервал берется в окрестности выборочного среднего, расчет которого нами был рассмотрен в кванте 49. Следует отметить, что доверительный интервал расширяется (уменьшается точность) при увеличении надежности (увеличивается x) и сужается (увеличивается точность) при увеличении объема выборки.Пример 52.1Случайная величина распределена нормально со среднеквадратичным отклонением 
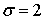. Найти доверительный интервал для оценки математического ожидания по выборочному среднему (объем выборки 100) с надежностью 0,99.Для надежности 0,99 величина 
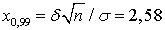. Отсюда находим 
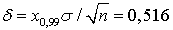.Замечание. Мы рассмотрели задачу нахождения доверительного интервала по заданным надежности и объему выборки. Возможны и другие постановки задачи. Если задана надежность γ и точность δ, то с помощью формулы 
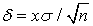можно определить минимальный объем выборки, необходимый для реализации заданной точности с заданной надежностью: 
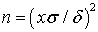. Если задана точность δ и объем выборки n, то можно определить надежность:
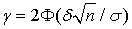.Если среднеквадратичное отклонение нормального распределения значений случайной величины в генеральной совокупности неизвестно, то пользоваться написанными выше формулами нельзя. Для решения этого вопроса рассмотрим случайную величину 
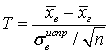, которая имеет уже не нормальное распределение, а распределение Стьюдента с n - 1 степенями свободы. Все использованные здесь обозначения уже были введены нами ранее. В итоге имеем, что вероятность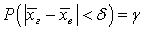 
, только определяется она уже не функцией Лапласа, а функцией распределенияСтьюдента, значение которой может быть взято из таблицы (см. ниже).
n |
γ |
n |
γ |
||||
0 ,95 |
0,99 |
0,999 |
0 ,95 |
0,99 |
0,999 |
||
5 |
2 ,78 |
4,60 |
8,61 |
20 |
2,093 |
2,861 |
3,883 |
6 |
2 ,57 |
4,03 |
6,86 |
25 |
2,064 |
2,797 |
3,745 |
7 |
2 ,45 |
3,71 |
5,96 |
30 |
2,045 |
2,756 |
3,659 |
8 |
2 ,37 |
3,50 |
5,41 |
35 |
2,032 |
2,720 |
3,600 |
9 |
2 ,31 |
3,36 |
5,04 |
40 |
2,023 |
2,708 |
3,558 |
10 |
2 ,26 |
3,25 |
4,78 |
45 |
2,016 |
2,692 |
3,527 |
11 |
2 ,23 |
3,17 |
4,59 |
50 |
2,009 |
2,679 |
3,502 |
12 |
2 ,20 |
3,11 |
4,44 |
60 |
2,001 |
2,662 |
3,464 |
13 |
2 ,18 |
3,06 |
4,32 |
70 |
1,996 |
2,649 |
3,439 |
14 |
2 ,16 |
3,01 |
4,22 |
80 |
1,001 |
2,640 |
3,418 |
15 |
2 ,15 |
2,98 |
4,14 |
90 |
1,987 |
2,633 |
3,403 |
16 |
2 ,13 |
2,95 |
4,07 |
100 |
1,984 |
2,627 |
3,392 |
17 |
2 ,12 |
2,92 |
4,02 |
120 |
1,980 |
2,617 |
3,374 |
18 |
2 ,11 |
2,90 |
3,97 |
∞ |
1,960 |
2,576 |
3,291 |
19 |
2 ,10 |
2,88 |
3,92 |
|
|
|
|
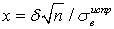, затем из этой формулы определяют доверительный интервал δ. Процедура аналогична, рассмотренной выше, с той лишь разницей, что среднеквадратичное отклонение здесь неизвестно, а вместо него рассчитывается «исправленное» выборочное среднеквадратичное отклонение 
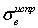. Ввиду этого и закон распределения вероятностей случайной величины T оказывается иным.Видеолекция «Интервальные оценки»: 
