43.
Центральная предельная теорема
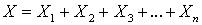есть сумма большого числа взаимно независимых случайных величин 
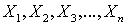, влияние каждой из которых на сумму ничтожно мало, то X имеет распределение близкое к нормальному.Пусть 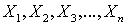— независимые случайные величины, каждая из которых имеет конечные математическое ожидание и дисперсию:
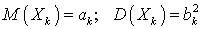.Обозначим 
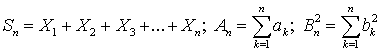.Для нормированной суммы 
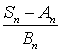функция распределения есть:
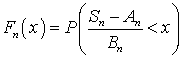.К последовательности случайных величин 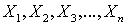применима центральная предельная теорема, если при любом x функция распределения нормированной суммы 
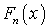стремится к нормальной функции распределения при 
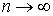, т.е.:
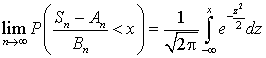.В частности, если все случайные величины 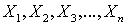одинаково распределены, а их дисперсии конечны и отличны от нуля, то к 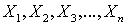применима центральная предельная теорема
.Ляпунов
показал, что, если для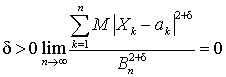 
, то к последовательности 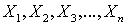применима центральная предельная теорема.Пример 43.1Монета подбрасывается 10000 раз. Найти вероятность того, что относительная частота выпадения орла отличается от 0,5 не меньше, чем на 0,01.Решение.Надо найти 
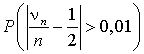, где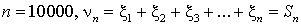 
— число выпадений герба, 
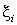— независимые случайные величины, определяющие количество выпадений орла при «итом» испытании. Для каждой 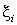математическое ожидание — 
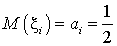, а дисперсия — 
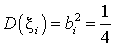. В силу центральной предельной теоремы величина 
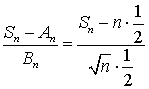имеет распределение, близкое к нормальному:
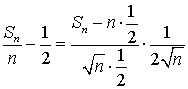.Следовательно, неравенство 
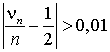можно записать в виде:
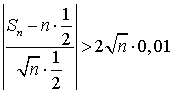.Учитывая, что 
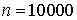, получим: 
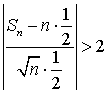.Следовательно, искомая вероятность равна:
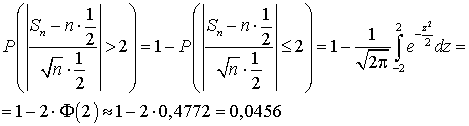. Видеолекция «Центральная предельная теорема»: 
