22.
Интегральная теорема Лапласа
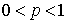Пусть имеется n независимых испытаний, каждое с двумя исходами. Вероятности удачи и неудачи равны, соответственно, и 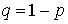, то есть выполнены все условия для применения формулы Бернулли. Пусть число испытаний n велико, и формула Бернулли, таким образом, становится неудобной в применении. В кванте 21 мы рассмотрели локальную предельную теорему Лапласа, позволяющую приближенно рассчитать вероятность наступления ровно k удач. Предположим, что нас интересует вероятность того, что число удач будет не менее чем k1 и не более, чем k2, или, для краткости, от k1до k2 раз. Ответ на этот вопрос дает следующая теорема.Теорема (интегральная теорема Лапласа). Если вероятность удачи p в одном из n независимых испытаний с двумя исходами постоянна и отлична от нуля и единицы, то вероятность появления от k1до k2 удач приближенно равна (тем точнее, чем больше n):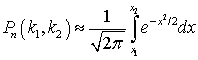,где 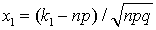, 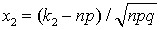.Без доказательства.Замечание 1. Как и в случае с локальной теоремой Лапласа, этой формулой при больших n пользоваться удобней, чем формулой Бернулли, поскольку она не содержит вычисления факториалов от больших чисел.Замечание 2. Интеграл, содержащийся в рассмотренной теореме, не может быть вычислен в элементарных функциях, то есть он относится к классу так называемых «не берущихся» интегралов. Его значение может быть определено численно, например, с использованием одного из вычислительных пакетов, или из таблицы для значений интеграла 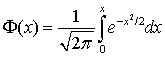, называемого функцией Лапласа. Ниже, в таблице 22.1, приведены некоторые значения функции Ф(x).

Таблица 22.1

Некоторые значения функции Лапласа Ф (x)

x

Ф (x)

x

Ф (x)

x

Ф (x)

0,0

0,00

0,6

0,23

1,2

0,38

0,1

0,04

0,7

0,26

1,3

0,40

0,2

0,08

0,8

0,29

1,4

0,42

0,3

0,12

0,9

0,32

1,5

0,43

0,4

0,16

1,0

0,34

2,0

0,48

0,5

0,19

1,1

0,36

2,5

0,49

 

 

 

 

5

0,499997

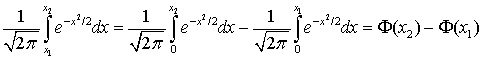Некоторые значения функции Лапласа Ф (x)При аргументе x > 5 значение функции Лапласа практически не отличается от 0,5. Функция Ф (x) при отрицательных значениях аргумента может быть вычислена по формуле для нечетной функции Ф(-x) = -Ф(x). Заметим также, что:. Используя обозначение для функции Лапласа, интегральная теорема Лапласа может быть записана в ви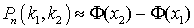де:, где 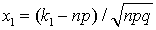, 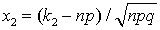. Пример 22.1Вероятность того, что деталь будет забракована, равна 0,2. Найти вероятность того, что среди 1000 случайно отобранных деталей окажется от 100 до 200 бракованных.Будем исходить из того, что в результате испытания имеется два исхода: удача с вероятностьюp = 0,2 — когда будет найдена бракованная деталь, и неудача с вероятностьюq = 0,8 — в другом случае. Всего производится 1000 независимых испытаний и требуется посчитать вероятность 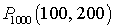.Воспользуемся интегральной теоремой Лапласа: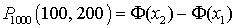, где 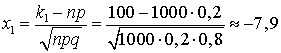, 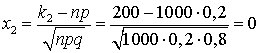. В итоге имеем: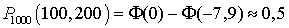.  Видеолекция «Интегральная теорема Лапласа»:
Перейти к выполнению теста: Интегральная теорема Лапласа. Тест
В начало