50.
Генеральная и выборочная дисперсия
Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения 
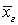.Если всех значения 
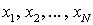различны, то:
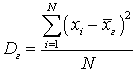.Если значение xi встречается с частотой Ni, то:
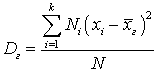,при этом 
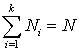.Определение. Генеральным среднеквадратичным отклонением называют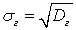 
.Определение. Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений значений признака в выборке от их выборочного среднего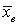 
.Если всех значения 
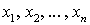различны, то:
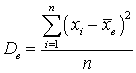.Если значение xi встречается с частотой ni, то:
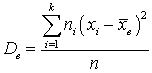,при этом 
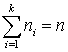.Определение. Выборочным среднеквадратичным отклонением называют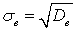 
.Теорема. Дисперсия (выборочная или генеральная) равна разности среднего от квадратов и квадрата от средней 
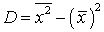.Доказательство.
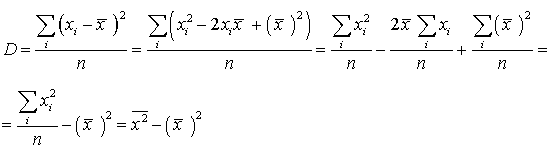.Теорема доказана.Для оценки генеральной дисперсии по выборке естественно было бы выбрать соотношение 
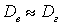, однако, такая оценка является смещенной, то есть математическое ожидание случайной величины — выборочной дисперсии — не равно групповой дисперсии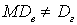 
. Действительно, вычислим:
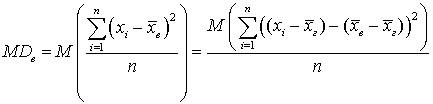.Здесь мы воспользовались свойством, что постоянный множитель можно выносить за знак математического ожидания, а далее воспользуемся тем, что математическое ожидание от суммы равно сумме математических ожиданий:
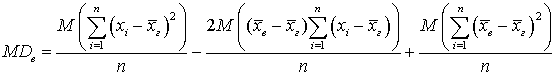.Внося знак математического ожидания под знак суммы в первом слагаемом, получим сумму nгенеральных дисперсий, и после деления на знаменатель первое слагаемое оказывается Dг:
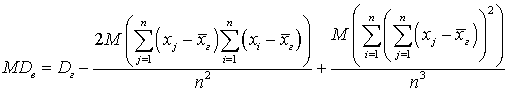.В этом выражении также использовано, что 
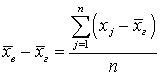. Далее предполагаем, что случайные величины — значение признака xi — независимы. Перемножение двух сумм во втором слагаемом и возведение в квадрат в третьем даст перекрестные члены (с разным номером i в сумме) и полные квадраты. Ввиду предположенной независимости случайных величин, математическое ожидание от произведений 
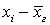с различными i будет равно произведению математических ожиданий, каждое из которых — нуль (вычисляется математическое ожидание отклонения случайной величины от математического ожидания). Полные же квадраты останутся, в результате чего имеем:
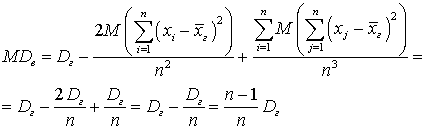.Мы получили, что математическое ожидание случайной величины — выборочной дисперсии — не равно генеральной дисперсии. Однако, как легко видеть, оценку можно «исправить», то есть в качестве оценки генеральной дисперсии брать «исправленную» выборочную дисперсию:
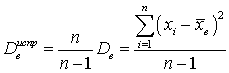,которая уже будет несмещенной оценкой. Видно, что «исправленная» выборочная дисперсия отличается от обычной знаменателем. При большом объеме выборки разница между ними стирается, и можно пользоваться любой. При n < 30 для оценки генеральной дисперсии используют «исправленную» выборочную. Аналогично оценке генерального среднего, оценка генеральной дисперсии в виде «исправленной» выборочной дисперсии является состоятельной, то есть при достаточно большом объеме выборки различия в выборочной дисперсии разных выборок будут малы и будут достаточно точно описывать генеральную дисперсию.Определение. «Исправленным» выборочным среднеквадратичным отклонением называют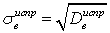 
.Замечание. «Исправленное» выборочное среднеквадратичное отклонение 
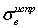не является несмещенной оценкой среднеквадратичного отклонения генеральной совокупности.Видеолекция «Генеральная и выборочная дисперсия»: 
