38.
Нормальное распределение
называется распределение вероятностей случайной величины X, плотность распределения вероятностей которой имеет вид:
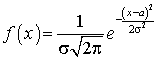.Коэффициент 
перед экспонентой обеспечивает выполнение равенства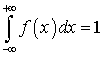 
.
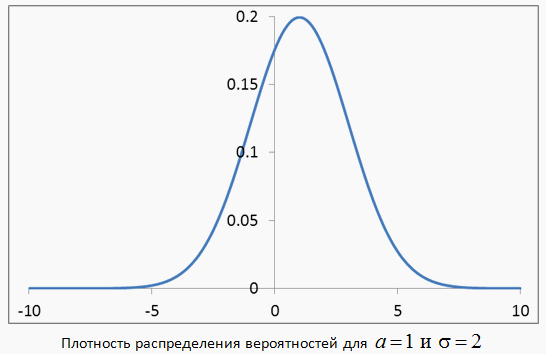Нормальное распределение характеризуется двумя параметрами: a и σ. Они однозначно определяют нормальное распределение.Нормированным называется нормальное распределение с параметрами a = 0 и σ = 1 . Если для нормально распределенной случайной величины X имеются a и σ, то 
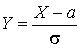— нормированная нормально распределенная случайная величина.Функция распределения F (x) для нормально распределенной случайной величины есть (квант 33):
,а для нормированного распределения —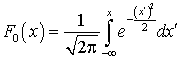
.Легко убедиться, что 
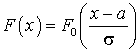, поэтому, поскольку таблица для функции F0 (x) имеется, по ней можно вычислить F (x).Математическое ожидание для нормально распределенной случайной величины может быть вычи c лено по формуле (квант 34):
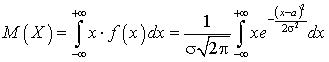.Используя метод замены переменной 
, получим: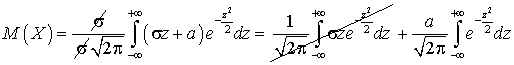
.Первое слагаемое равно нулю (нечетная функция под интегралом), а второе слагаемое равно a (
— интеграл Пуассона
). Следовательно, для нормального распределения:
Дисперсия для равномерно распределенной случайной величины с учетом, что может быть вычислено по формуле (квант 35):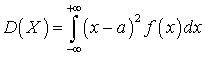
.
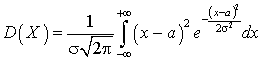.Введем переменную 
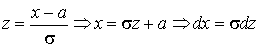. Получим 
.Интегрируя по частям, получим: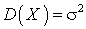
.Отсюда следует, что среднеквадратичное отклонение равно:
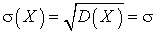. Видеолекция «Нормальное распределение»: 
