33.
Математическое ожидание непрерывной случайной величины
X |
x1 |
x2 |
x3 |
x4 |
… |
xn |
P |
p1 |
p2 |
p3 |
p4 |
… |
pn |
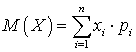. Для непрерывной случайной величины попробуем ввести аналогичное понятие. Пусть все возможные значения случайной величины X принадлежат отрезку [a, b]. Разобьем всю область значений, которые может принимать непрерывная случайная величина X на отдельные отрезки 
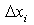и выберем внутри каждого отрезка точку 
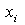. Сумма произведений различных значений 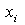на вероятность попадания в интервал 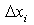есть 
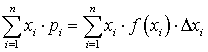. Переходя к пределу при стремлении к нулю величины максимального интервала 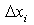получим определенный интеграл 
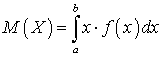.Определение. Математическим ожиданием случайной величины
X, все возможные значения которой принадлежат отрезку [a, b], называют определенный интеграл: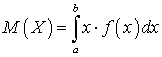
.Если возможные значения случайной величины X принадлежат всей числовой оси, то:
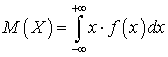.При этом предполагается, что несобственный интеграл сходится абсолютно, что означает существование интеграла 
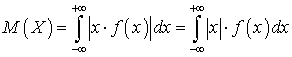.Пример 33.1Вычислить математическое ожидание случайной величины, плотность распределения которой имеет вид:
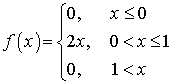.Решение. 
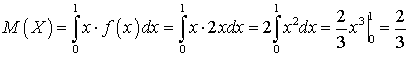.Пример 33.2Вычислить математическое ожидание случайной величины, плотность распределения которой имеет вид:
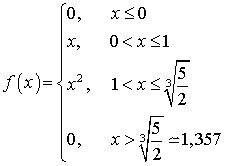.Решение.
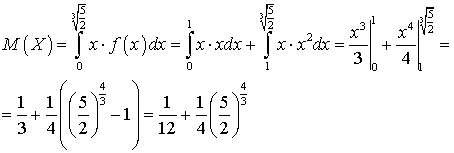.Пример 33.3Вычислить математическое ожидание случайной величины, плотность распределения которой имеет вид:
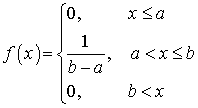.Решение. 
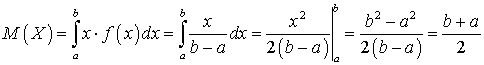. Видеолекция «Математическое ожидание непрерывной случайной величины»: 
