34.
Дисперсия непрерывной случайной величины
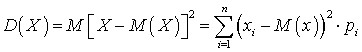, введем понятие дисперсии для непрерывной случайной величины.Определение. Дисперсией непрерывной случайной величины
называют математическое ожидание квадрата разности между этой случайной величиной и ее математическим ожиданием:
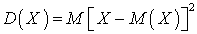.Воспользовавшись формулой для математического ожидания непрерывной случайной величины, возможные значения которой принадлежат отрезку [a, b] (см. квант 34) получим:
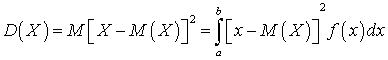.Если возможные значения принадлежат всей числовой оси, то:
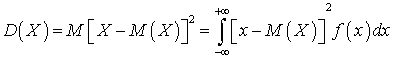.Из определения для дисперсии непрерывной случайной величины можно получить формулу, аналогичную той, что справедлива для дисперсии дискретной случайной величины:
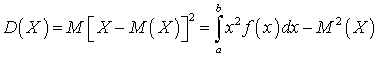,а для дисперсии случайной величины, возможные значения которой принадлежат всей оси, получим: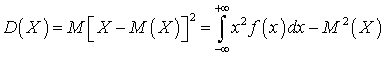
.Среднеквадратичное отклонение для непрерывной случайной величины определяется так же, как и для дискретной случайной величины: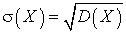
.Пример 34.1Вычислить дисперсию и среднеквадратичное отклонение случайной величины, плотность распределения которой имеет вид:
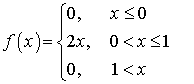.Решение.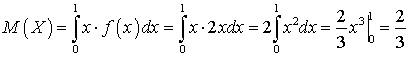 
.
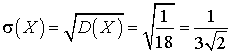.Пример 34.2Вычислить дисперсию и среднеквадратичное отклонение случайной величины, плотность распределения которой имеет вид:
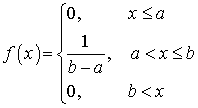.Решение.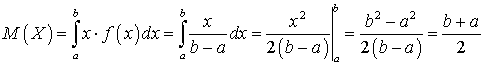 
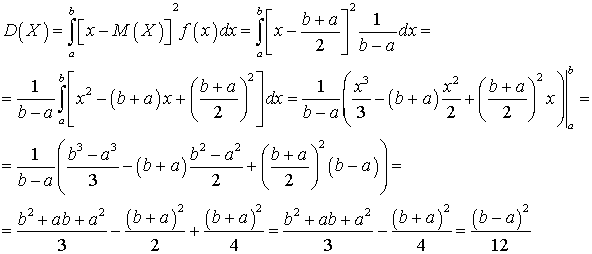
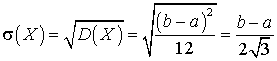Видеолекция «Дисперсия непрерывной случайной величины»: 
