37.
Показательное распределение
называется распределение вероятностей случайной величины X, плотность распределения вероятностей которой имеет вид:
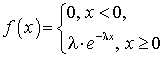,где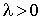 
— параметр показательного распределения.
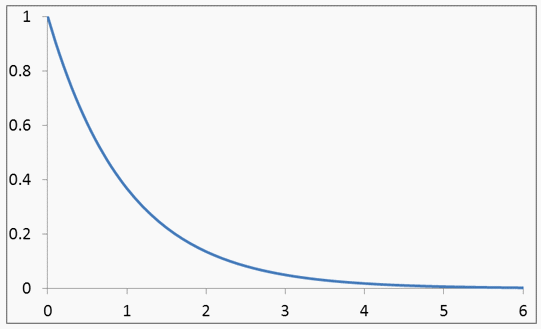Множитель 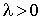перед экспонентой обеспечивает выполнение соотношения 
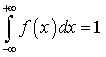.Вычислим функцию распределения F (x). Для этого воспользуемся формулой (квант 33):
.
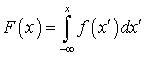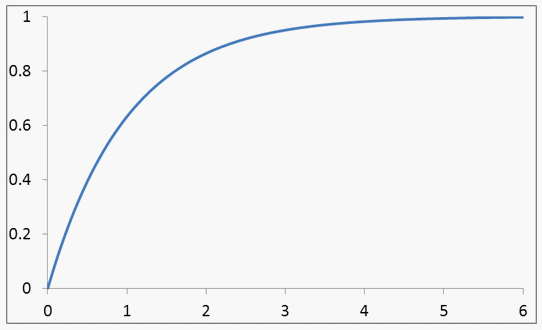Пусть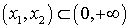 
. Вычислим вероятность попадания в интервал (a, b) случайной величины X, распределенной по показательному закону. По формуле (квант 33) 
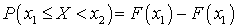получим
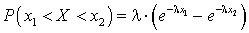.Пример 37.1Непрерывная случайная величина X распределена по показательному закону 
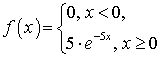. Найти вероятность того, что в результате испытаний X попадет в интервал (1, 2).Решение.
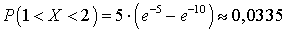Математическое ожидание для случайной величины, которая распределена по показательному закону, может быть вычичлено по формуле (квант 34):
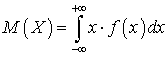.Интегрируя по частям, получим:
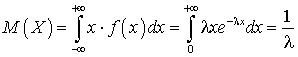.Дисперсия для для случайной величины, которая распределена по показательному закону, может быть вычислено по формуле (квант 35):
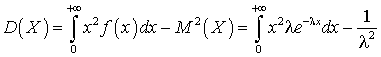.Интегрируя по частям, получим:
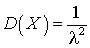.Отсюда следует, что среднеквадратичное отклонение равно:
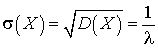. Видеолекция «Показательное распределение»: 
