36.
Равномерное распределение
на интервале (a, b) называется такое распределение случайной величины, все значения которой лежат на этом интервале, а плотность распределения вероятностей f (x) равна постоянной величине внутри этого интервала и нулю за его пределами:
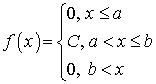.Найдем значение константы С. Для этого воспользуемся свойством функции f (x) (квант 33):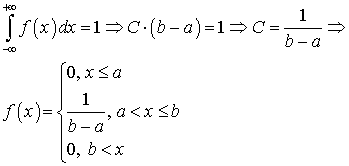
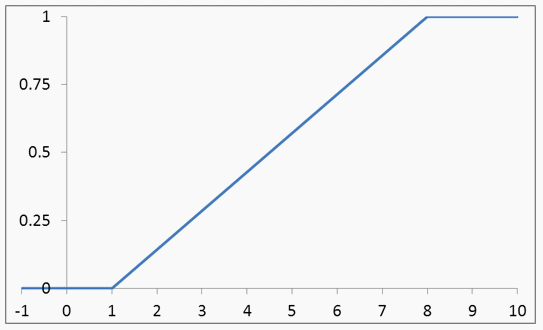
Вычислим для равномерной случайной величины функцию распределения F (x). Для этого воспользуемся формулой (квант 33):
. 
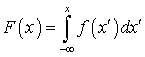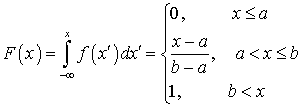
Пусть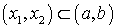 
. Вычислим вероятность попадания равномерно распределенной случайной величины X в интервал (a, b):
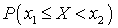По формуле (квант 33) 
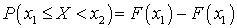получим:
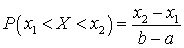.Математическое ожидание для равномерно распределенной случайной величины может быть вычичлено по формуле (квант 34) 
.
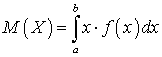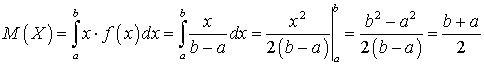.Дисперсия для равномерно распределенной случайной величины может быть вычислено по формуле (квант 35):
.
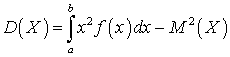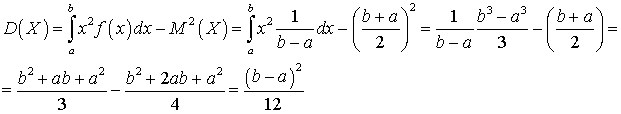.Среднеквадратичное отклонение равномерно распределенной случайной величины может быть вычиcлено по формуле (квант 35):
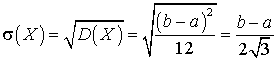. Видеолекция «Равномерное распределение»: 
