56.
Метод Монте-Карло
или, по-другому, метод статистических испытаний, используется в различных областях: математике, физике, биологи, экономике и т.п. Суть метода состоит в разыгрывании случайной величины (генерации случайных чисел с требуемым законом распределения) и вычислении того или иного результата, зависящего от значений случайной величины. Пусть требуется вычислить некоторое значение a. Для его вычисления вводят такую случайную величину X, чтобы ее математическое ожидание было MX = a. Далее производится некоторое количество испытаний , в результате которых рассчитываются значения xi этой случайной величины и в качестве оценки неизвестной берется среднее арифметическое значений xi. Это можно трактовать следующим образом: из генеральной совокупности с генеральным средним a делается выборка из объектов и неизвестное значение a оценивается как выборочное среднее. Если генеральная совокупность имеет нормальное распределение, то на основании интервальных оценок, изложенных в кванте 52, мы можем определить доверительный интервал, который покрывает неизвестное a с вероятностью γ: 
. В случае, когда среднеквадратичное отклонение σ нормального распределения генеральной совокупности известно, то доверительный интервал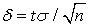 
, где t — аргумент функции Лапласа
в уравнении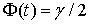 
. В случае, когда σ неизвестно, то в качестве него берут «исправленное» выборочное среднеквадратичное отклонение, и доверительный интервал вычисляется по той же формуле: 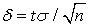, но только величина t определяется из распределения Стьюдента, и может быть найдена по таблице, приведенной в кванте 52. Если закон распределения генеральной совокупности имеет вид отличный от нормального, то при достаточно большой выборке (n > 30) можно пользоваться указанными формулами, причем различие между ними становится уже несущественным.Для разыгрывания случайной величины используют компьютерные генераторы случайных чисел. Строго говоря, они не являются генераторами истинно случайных чисел, поскольку через некоторый (хотя и достаточно большой) период числа будут повторяться. Поэтому иногда говорят о псевдослучайных числах. Если розыгрышей проводится меньше, чем период повторения (так чаще всего и бывает), то эти числа практически неотличимы от случайных, и в дальнейшем мы будем говорить о них, как о случайных числах. Обычно генератор случайных чисел выдает случайные числа ξ с равномерным распределением в диапазоне от нуля до единицы. Если требуется другой диапазон, то делают линейное преобразование x =aξ +b. Эти случайные числа имеют также равномерное распределение, но уже в диапазоне от b до a +b. Выбирая постоянные a и b, можем получить любой диапазон изменения значений случайной величины.Для моделирования дискретной случайной величины с законом распределения, отличным от равномерного (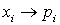
), поступают следующим образом: диапазон [0, 1) разбивают на примыкающие друг к другу участки длиной 
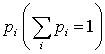, и если генератор случайных чисел выдает число в i-м диапазоне, то случайной величине X присваивают значение xi. В частности, для моделирования случайной величины имеющей два значения (вероятность удачи p и вероятность неудачи q = 1 - p) диапазон [0, 1) нужно разбить на два участка (0, p) и (p, 1) с длинами p и q соответственно. Если генератор случайных чисел выдаст число в 1 диапазоне, то это моделируется как удача, если число из 2 диапазона, то как неудача.Если требуется смоделировать непрерывную случайную величину с функцией распределения F (x), исходя из равномерно распределенной последовательности случайных чисел в диапазоне [0, 1), то это делают на основании следующей теоремы.Теорема. Если ξ случайные числа из диапазона [0, 1) с равномерным распределением, то значения непрерывной случайной величины x с функцией распределения F (x) могут быть получены как решения уравнения F (x) = ξ.Доказательство.Как было установлено в кванте 31 функция распределения непрерывной случайной величины это монотонно возрастающая от 0 до 1 функция. Поэтому, используя обозначение 
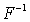для обратной функции, можем записать решение: 
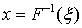, причем в силу монотонности функции это решение — единственное. Покажем, что значения случайной величины X, определяемые таким образом, будут соответствовать функции распределения F (x). Если случайная величина — с <X <d, то в силу монотонного возрастания F (x) случайная величина 
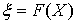удовлетворяет неравенству 
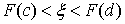. Отсюда имеем, что:
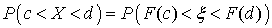.Так как ξ имеет равномерное распределение в диапазоне от 0 до 1, то 
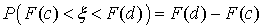, а, значит, 
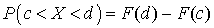, что и означает, что случайная величина X имеет функцию распределения F (x). Теорема доказана.Таким образом, для получения случайной величины с функцией распределения F (x) достаточно посчитать значения 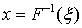, где ξ — случайные числа из диапазона (0, 1) с равномерным распределением, выдаваемые компьютером.Отдельно рассмотрим разыгрывание нормально распределенной случайной величины. Легко получить, что в случае равномерного распределения в диапазоне от 0 до 1 математическое ожидание 
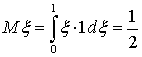, дисперсия 
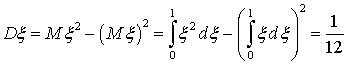. Составим сумму независимых, равномерно распределенных на [0, 1) случайных величин 
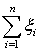. Используя свойства математического ожидания и дисперсии, легко получить, что математическое ожидание суммы равно n / 2, а дисперсия суммы равна n / 12. Введем в рассмотрение случайную величину 
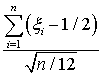, которая имеет нулевое математическое ожидание и единичную дисперсию. В силу центральной предельной теоремы при 
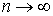распределение этой случайной величины будет стремиться к нормальному с нулевым математическим ожиданием и единичной дисперсией. Взяв достаточно большое n (порядка 10 и более) будем иметь распределение, близкое к нормальному. Если требуется получить нормальное распределение с математическим ожиданием a и среднеквадратичным отклонением σ, то в качестве случайной величины берут 
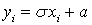. Легко проверить, что распределение случайной величины Y действительно будет нормальным с математическим ожиданием a и среднеквадратичным отклонением σ.Видеолекция «Метод Монте-Карло»: 
