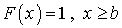Теория вероятностей и математическая статистика: Функция распределения вероятностей непрерывной случайной величины

31.

Функция распределения вероятностей непрерывной случайной величины

Пусть X — непрерывная случайная величина, возможные значения которой заполняют интервал (a, b). Для дискретной случайной величины распределение задается таблицей:

X	x₁	x₂	x₃	x₄	…	x_n
P	p₁	p₂	p₃	p₄	…	p_n

Для непрерывной случайной величины X таблицу построить нельзя. Для нее вводится понятие функции распределения.Определение. Функцией распределения непрерывной случайной величины

X называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значений, меньшее x, т.е.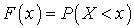

. Геометрическая интерпретация:

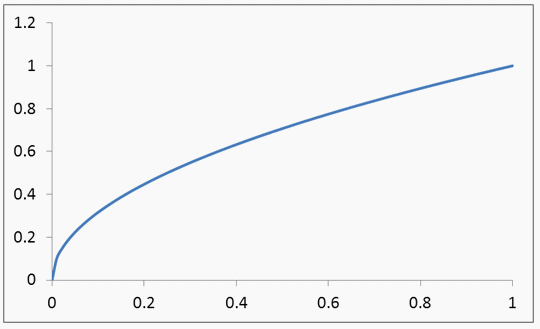При заданном x значение функции F(x) определяет вероятность того, что случайная величина X при испытании примет значение, меньшее, чем F(x).Определение. Случайную величину X называют непрерывной

, если ее функция распределения F(x) есть непрерывная кусочно-дифференцируемая функция с непрерывной производной.Свойства функции распределенияСвойство 1. Значения функции распределения F(x) случайной величины Xнаходятся в диапазоне от 0 до 1, то есть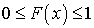

. Доказательство. Поскольку по определению

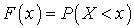, где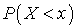

— вероятность, что случайная величина X примет значение меньше, чем x, а вероятность лежит в диапазоне от 0 до 1, то

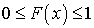.Свойство 2. Функция распределения F (x) является неубывающей.Доказательство. Пусть

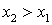, тогда:

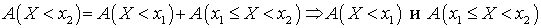Поскольку они несовместны, то:

. Следствие 1. Вероятность того, что случайная величина Х примет значение в диапазоне (a, b), равна приращению ее функции распределения на этом интервале: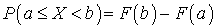

. Данная формула напоминает формулу

Ньютона

—Лейбница

.Пример 31.1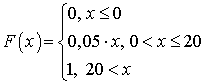

. Найти вероятность того, что Х примет значение в диапазоне (2, 6)

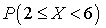Решение.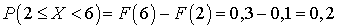

.Следствие 2. Вероятность того, что непрерывная случайная Величина Х примет одно предельное значение равна 0.Положим в формуле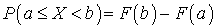

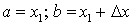. Получим:

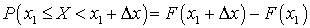. Пусть

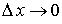. Поскольку функция F (x) — непрерывна, то:

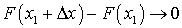при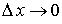

.Замечание 1. Равенство вероятности нулю не означает невозможности события.Замечание 2. Нет смысла говорить о вероятности одного значения. Надо говорить о вероятности попадания в интервал.Свойство 3. Если возможные значения случайной величины Х принадлежат интервалу (a, b) , то:

;

Доказательство. Пусть

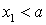, тогда событие

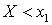— невозможное. Следовательно,

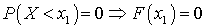. Пусть

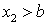, тогда событие

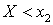— достоверное. Следовательно,

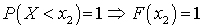.Следствие. Если возможные значения Х — вся числовая ось, то:

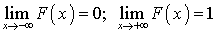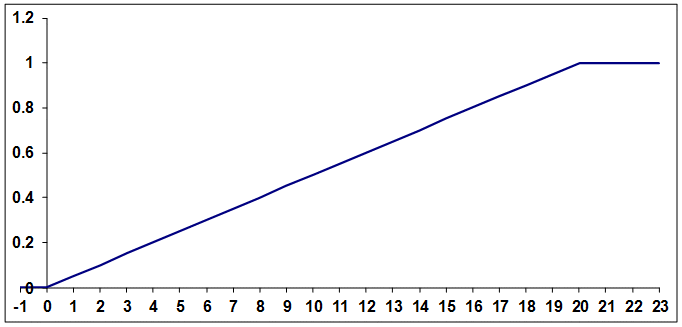
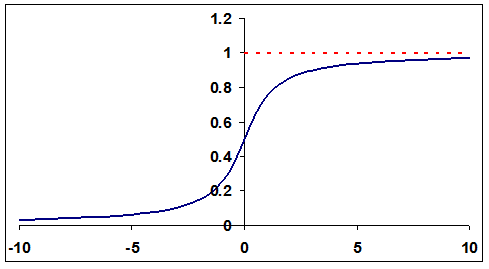Если возможные значения случайной величины Х принадлежат интервалу (a, b) , то график функции распределения имеет вид

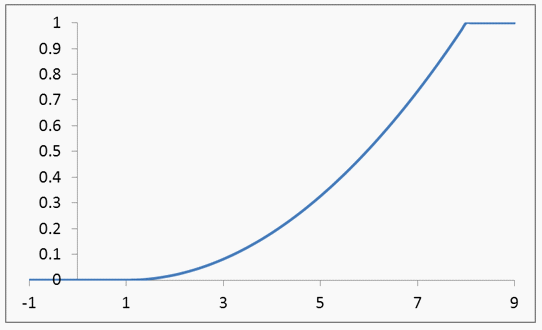Замечание 3. Для дискретной случайной величины график функции распределения — ступенчатая функция.Пример 31.2Найти P (2 < X < 3), если функция распределения имеет вид:

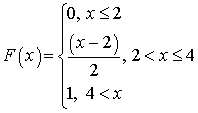.Решение..

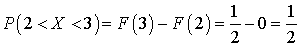Видеолекция «Функция распределения вероятностей непрерывной случайной величины»:

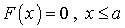Перейти к выполнению теста: Функция распределения вероятностей непрерывной случайной величины. Тест