28.
Задачи на дискретные случайные величины
Пример 28.1Заданы две случайных величины с законами распределения:

X

1

2

3

p

0,2

0,5

0,3

Y

-1

0

0,5

2

p

0,1

0,2

0,4

0,3

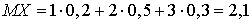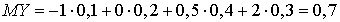Найти математическое ожидание и дисперсию каждой из них.Вычисляем по определению математического ожидания:,.Вычислим дисперсию по формуле для случайной величиныX, и аналогичной — для Y. Для этого посчитаем: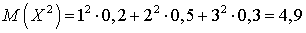, 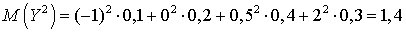. Следовательно: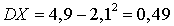, 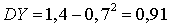. Пример 28.2Вычислить 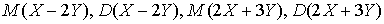для независимых случайных величин, заданных в предыдущей задаче.Используя свойства математического ожидания и дисперсии, а также найденные в предыдущей задаче значения, получаем: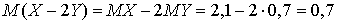, , 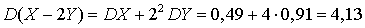, 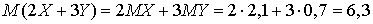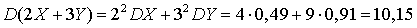. Пример 28.3Известно, что некоторая случайная величина может принимать значения 0, 2 и 4. Известно, что математическое ожидание равно 2, а дисперсия — 0,8. Найти закон распределения случайной величины.Обозначим вероятности, стоящие в законе распределения, следующим образом:

X

0

2

4

p

p1

p2

p3
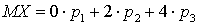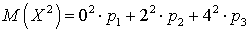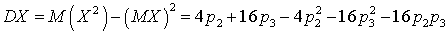Вычисляем:,,.Кроме того, используем условие: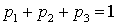. В итоге имеем систему: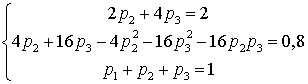. Выражая из первого уравнения 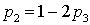и подставляя во второе после сокращения, получим уравнение 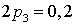. Находя p1 и p2 из первого и третьего уравнений, запишем ответ: 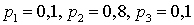. Пример 28.3Подбрасывают два игральных кубика. Найти закон распределения, математическое ожидание и дисперсию случайной величины — суммы выпавших очков.Вероятность выпадения любой заданной цифры на одном кубике равна 1/6. Ввиду независимости кубиков вероятность выпадения двух заданных цифр на двух кубиках есть произведение вероятностей выпадения на каждом из кубиков, то есть 1/36.Сумма очков 2 может получиться только при выпадении 1 — 1, то есть с вероятностью 1/36. Сумма очков 3 может получиться при выпадении 1 — 2 и 2 — 1 и, ввиду несовместности событий, происходит с вероятностью 2/36. Сумма очков 4 может получиться при выпадении 1 — 3, 3 — 1, 2 — 2 с вероятностью 3/36. Продолжая в том же духе, получим закон распределения:

Сумма

2

3

4

5

6

7

8

9

10

11

12

p

1/36

2/36

3/36

4/36

5/36

6/36

5/36

4/36

3/36

2/36

1/36

Для проверки убеждаемся, что сумма вероятностей равна единице.Далее, используя найденный закон распределения, можем по определению получить математическое ожидание и дисперсию. Однако поступим проще, запишем рассматриваемую случайную величину X как сумму двух случайных величин X1 + X2, представляющих собой число выпавших очков на каждом из кубиков. Очевидно, что законы распределения, математические ожидания и дисперсии случайных величин X1 и X2 одинаковы, и были нами вычислены в кванте 25, кванте 26 и кванте 27 (). Случайные величины X1 и X2 независимы, а, значит: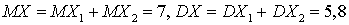. Пример 28.4Имеется три независимо работающих устройства. Вероятность того, что устройство выйдет из строя за некоторый промежуток времени, равна 0,2, 0,4 и 0,7 для 1, 2 и 3 устройств, соответственно. Найти закон распределения, математическое ожидание и дисперсию случайной величины — числа вышедших из строя устройств.Случайная величина может принимать значения 0, 1, 2 и 3. Вероятность того, что все три независимых устройства выйдут из строя, равна 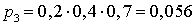. Вероятность того, что ни одно из устройств не выйдет из строя равна 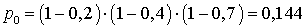. Вероятность того, что только одно устройство выйдет из строя равна: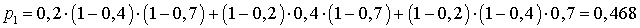. Вероятность того, что ровно два устройства выйдут из строя, можно посчитать по формуле, аналогичной p3, а можно и из условия, что сумма всех вероятностей равна единице. В обоих случаях получим p2 = 0,332. Таким образом, имеем закон распределения:

X

0

1

2

3

p

0,144

0,468

0,332

0,056

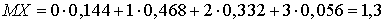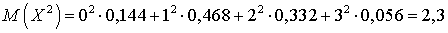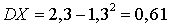На основании закона распределения вычисляем:, , .  Видеолекция «Задачи на дискретные случайные величины»:
Перейти к выполнению теста: Задачи на дискретные случайные величины. Тест
В начало