Теория вероятностей и математическая статистика: Математическое ожидание дискретной случайной величины

26.

Математическое ожидание дискретной случайной величины

Наиболее полная возможная информация о дискретной случайной величине

содержится в законе распределения

. Однако в ряде случаев этот закон распределения неизвестен, или его нахождение сопряжено со значительными трудностями, поэтому наряду с законом распределения для характеристики случайной величины широко используют такие понятия как математическое ожидание

и дисперсия

. В этих понятиях содержится существенно меньше информации о случайной величине, чем в законе распределения, но в ряде случаев этой информации вполне достаточно, и эта информация часто является лучше воспринимаемой для понимания. В этом кванте мы рассмотрим математическое ожидание (для краткости иногда произносят «мат. ожидание»).Определение. Математическим ожиданием дискретной случайной величины

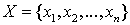с распределением вероятностей соответственно

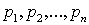называется величина:

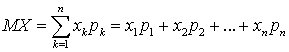. Замечание 1. Если дискретная случайная величина содержит бесконечное число возможных значений, то математическое ожидание будет содержать бесконечное число слагаемых в сумме, то есть будет числовым рядом

.Замечание 2. Величина X — случайная, то есть может принимать случайные значения, но математическое ожидание MX, вычисляемое на основе закона распределения, есть число не случайное, а имеющее для данного закона распределения вполне определенное значение.Пример 26.1Найти математическое ожидание случайной величины, заданной законом распределения:

x	2	3	5	6
p	0,1	0,3	0,1	0,5

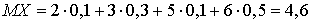По определению математического ожидания вычисляем:

. Пример 26.2Найти математическое ожидание случайной величины — числа выпавших очков при подбрасывании игрального кубика.В 25 кванте нами был получен закон распределения заданной случайной величины: вероятности каждого из возможных значений 1, 2, 3, 4, 5, 6 равны 1/6. По определению математического ожидания вычисляем:

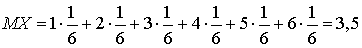. Несмотря на то, что возможные значения случайной величины — исключительно натуральные числа, математическое ожидание может быть числом не целым.Выясним вероятностный смысл математического ожидания. Пусть произведено достаточно большое число испытаний N. Случайная величина X в результате N испытаний m₁ раз приняла значение x₁, m₂ раз — значение x₂, и так далее: m_n раз — значение x_n. Очевидно, что

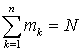. Вычислим среднее арифметическое случайной величины X:

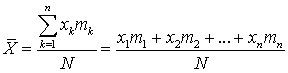. Записав это соотношение в виде:

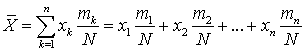, и вводя относительную частоту повторения

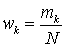, среднее арифметическое случайной величины запишется как:

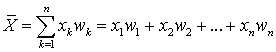. Если число испытаний N велико, то относительная частота повторений приблизительно равна вероятности выпадения этого значения случайной величины

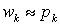, а, значит, среднее арифметическое случайной величины приблизительно равно ее математическому ожиданию

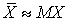. В этом и состоит вероятностный смысл математического ожидания.Сформулируем ряд свойств математического ожидания, упрощающих вычисления.

Математическое ожидание неслучайной величины равно этой величине, то есть MC = C.Действительно, неслучайную величину можно рассматривать как случайную, которая может принимать единственное значение С с вероятностью, равной единице. Тогда по определению математического ожидания получаем MC = C.
Постоянный множитель можно выносить за знак математического ожидания, то есть 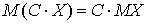.Величина 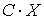есть случайная величина, в которой значения случайной величины X умножаются на константу C, а соответствующие вероятности остаются неизменными. Тогда в формуле для математического ожидания все значения случайной величины будут содержать множитель C, который можно вынести за скобку и получить сформулированное утверждение:.
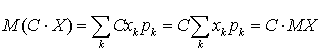Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, то есть: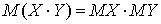. Пусть законы распределения случайных величин X и Y равны соответственно и 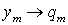. Тогда закон распределения случайной величины 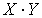будет 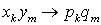(произведение ввиду того, что случайные величины независимы). По определению математического ожидания 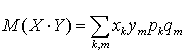, а 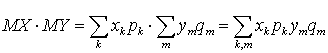. Отсюда и следует равенство 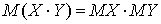. Аналогичную формулу можно получить и для произведения трех и более независимых случайных величин разбиением на пары множителей и последовательным применением этого свойства к каждой паре.
Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, то есть 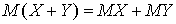.Используя обозначения, введенные в предыдущем пункте и обозначая вероятность того, что случайная величина 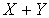примет значение 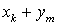символом 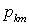можем записать: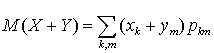. Перегруппируем слагаемые в сумме: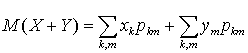. Величина есть сумма вероятностей того, что случайная величина Y примет значение y_m, а при этом случайная величина X имеет значение x_k. Все эти события несовместны, значит, . Аналогично можно показать, что 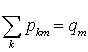. В итоге получаем: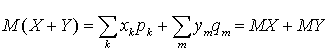.Аналогичная формула справедлива для суммы трех и более случайных величин, которую можно получить разбиением на пары случайных величин и последовательным применением полученной формулы для каждой из пар. Используя второе свойство легко показать, что .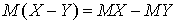