27.
Дисперсия дискретной случайной величины
В кванте 26 для характеристики случайной величины мы ввели понятие математического ожидания. При большом числе испытаний математическое ожидание приблизительно равно среднему значению случайной величины. Очевидно, что только математическое ожидание недостаточно характеризует случайную величину. В частности, можно привести два примера случайной величины с одинаковым математическим ожиданием (например, равным нулю), при этом разброс значений первой из них будет малым (все значения случайной величины расположены вблизи ее математического ожидания, то есть нуля), а разброс второй, наоборот, большим (значения случайной величины имеют большие значения по модулю, но при вычислении математического ожидания значения случайной величины разных знаков сокращаются между собой). Вся информация о случайной величине заложена в законе распределения, а математическое ожидание — это одна из характеристик закона распределения, и в ряде случаев недостаточная для описания случайной величины. Так возникает необходимость указать не только среднее значение случайной величины (примерно равное математическому ожиданию), но и ее разброс в окрестности этого среднего. Например, в стрельбе для описания того, насколько далеко «ложатся» друг от друга пули? используют понятие кучности, которое и характеризует разброс случайной величины — положения пробоины в мишени.Выясним теперь, как можно было бы описать разброс значений случайной величины. Можно ввести отклонение случайной величины от ее математического ожидания X - MX, которая также будет случайной величиной. Описать разброс как среднее отклонение оказывается невозможным, так как математическое ожидание отклонения M (X – MX) оказывается всегда равным нулю (это легко вычислить, используя свойства математического ожидания). И, действительно, отклонения разных знаков будут компенсировать друг друга. Что бы получить ненулевое среднее отклонение, можно говорить о модуле отклонения или квадрате отклонения. В обоих случаях эти случайные величины будут иметь только положительные значения, и не будут сокращаться при вычислении математического ожидания. При этом среднее значения модуля отклонения или квадрата отклонения будут характеризовать именно рассеяние случайной величины в окрестности ее математического ожидания. Обычно используют квадрат отклонения и вводят понятие дисперсии.Определение. Дисперсией дискретной случайной величины X называется величина 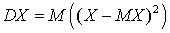. Замечание 1. Величина X — случайная, а дисперсия DX, так же, как и математическое ожидание MX, имеет для данного закона распределения вполне определенное значение.Замечание 2. Для закона распределения случайной величины дисперсию можно записать как 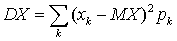.Замечание 3. Для расчета удобней пользоваться не формулой, фигурирующей в определении, а формулой, которую можно получить, используя свойства математического ожидания: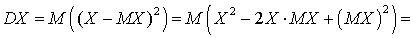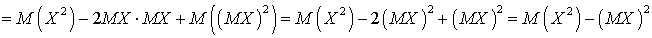. Пример 27.1Найти дисперсию случайной величины, заданной законом распределения:

x

2

3

5

6

p

0,1

0,3

0,1

0,5

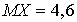В 26 кванте мы вычислили математическое ожидание случайной величины с таким законом распределения и получили . Вычислим дисперсию согласно определению: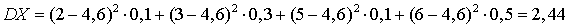.Вычислим теперь дисперсию с помощью формулы 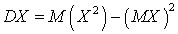. Величина и тогда получаем тот же ответ 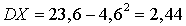.Пример 27.2Найти дисперсию случайной величины — числа выпавших очков при подбрасывании игрального кубика.В 25 кванте нами был получен закон распределения заданной случайной величины (вероятности каждого из возможных значений 1, 2, 3, 4, 5, 6 равны 1/6), а в 26 кванте — математическое ожидание (MX = 3,5). По определению дисперсии вычисляем: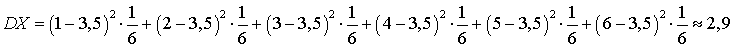.Для использования другой формулы для дисперсии вычисляем: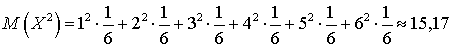.и тогда получаем тот же ответ: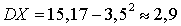.Сформулируем ряд свойств дисперсии, упрощающих вычисления.
  1. Дисперсия всегда неотрицательна, то есть 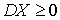. Это видно из определения дисперсии: в сумме присутствуют только неотрицательные слагаемые.
  2. Дисперсия неслучайной величины равна нулю, то есть 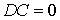.Очевидно из определения дисперсии и свойства для математического ожидания неслучайной величины.
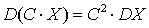  3. . Действительно,.
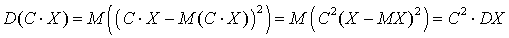  4. Дисперсия суммы или разности двух независимых случайных величин равна сумме их дисперсий, то есть . 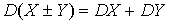Действительно,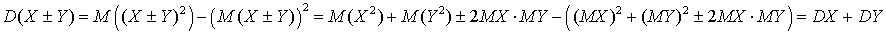. Аналогичная формула справедлива для суммы или разности трех и более случайных величин, которую можно получить разбиением на пары случайных величин и последовательным применением полученной формулы для каждой из пар.
Если случайная величина имеет размерность (например, для случайной величины дальности полета снаряда размерность есть метры или километры), то математическое ожидание имеет такую же размерность, а дисперсия имеет размерность квадрата от размерности случайной величины. Поэтому для характеристики рассеяния вводят величину, равную квадратному корню из дисперсии.Определение. Среднеквадратичным отклонением случайной величиныXявляется 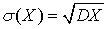.  Видеолекция «Дисперсия дискретной случайной величины»:
Перейти к выполнению теста: Дисперсия дискретной случайной величины. Тест
В начало