57.
Использование методов математической статистики в экономике
в экономике чрезвычайно широко и разнообразно. Мы ограничимся некоторыми примерами в достаточно простой постановке, что бы продемонстрировать возможности математической статистики.Одна из функций банков — это выдача кредитов. Человек, взявший кредит, долями возвращает его, а также платит определенный процент за пользование кредитом. В итоге через оговоренный промежуток времени человек возвращает всю сумму кредита и плату за его использование. Однако, по тем или иным обстоятельствам, некоторые люди не могут выполнить условия кредита. Конечно, банк может через суд наложить взыскание и тем самым компенсировать потери. Тем не менее, для банков более важным является выдача кредитов и извлечение из этого прибыли, а не наложение взыскания, поэтому для банков будет разумной стратегия выдавать кредит не в любом случае, а когда он может быть уверен, что условия кредита будут исполнены. Таким образом, возникает случайная величина — будет возвращен кредит или нет. Чтобы определить, кому выдать кредит, а кому — нет, банк анализирует статистическую информацию. Сюда входит и кредитная история самого человека, и процент вернувших кредит в срок той категории людей, к которой относится заемщик и тому подобное. Этот анализ и производится методами теории вероятностей и математической статистики — вычисление вероятности, вычисление среднего, дисперсии и т.д.Пример 57.1Банк выдает кредиты по 1 млн руб. сроком на 1 год. Вероятность невозврата кредита — 1%. Какую процентную ставку должен установить банк, чтобы в среднем иметь прибыль?Обозначим ставку, измеряемую в долях от единицы через p (соответствует 100 p%). Прибыль банка будет величиной случайной, поскольку кредит вместе с процентами клиент может вернуть, а может и не вернуть. Закон распределения этой случайной величины следующий:
p |
-1 |
0,99 |
0,01 |
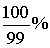(несколько больше, чем 1%).Другой пример — это выработка стратегии работы страховых компаний. Наступление или не наступление страхового случая — величина случайная. Страховая компания анализирует статистические данные по наступлению различных страховых случаев и условий, в которых они наступили. Таким образом, можно оценить вероятность наступления страхового случая у страхователя, и в зависимости от ее величины установить для него страховой взнос. Чем больше риск, тем больше будет страховой взнос. Его величина определяется страховой компанией так, чтобы в среднем расходы по наступлению страховых случаев данного типа были меньше, чем доходы в виде страховых взносов от страхователей.Пример 57.2Пусть страховая компания заключает договоры страхования сроком на 1 год на S руб. каждый. Страховой случай происходит с вероятностью p и не происходит с вероятностью q = 1 - p. Таким образом, имеем закон распределения случайной величины Xi — количества страховых случаев у одного (i-го) страхователя (0 — если страховой случай не наступил и 1 — если наступил):
0 |
1 |
q |
p |
, 
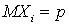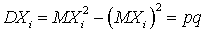. Случайная величина 
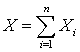— количество страховых случаев у страхователей имеет математическое ожидание 
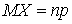и дисперсию 
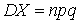. В силу центральной предельной теоремы случайная величина X распределена по нормальному закону. В среднем страховая компания должна будет выплатить npS страховых возмещений. Таким образом, если с каждого страхователя брать по pS руб. страхового взноса (100 p процентов от суммы S), то в среднем у страховой компании будет нулевой баланс. Разумеется, npS страховых возмещений — это величина случайная, и может оказаться как больше (у страховой компании будут убытки), так и меньше (у страховой компании образуется прибыль). Чтобы не было убытков, сумма страхового взноса должна быть больше, чем рассчитано, причем ее величину можно определить с помощью интервальных оценок. Обозначим реальную страховую ставку 
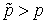. Тогда страховая компания соберет с n страхователей сумму 
рублей. Этой суммы хватит, чтобы возместить потери, связанные с наступлением страхового случая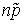 
клиентам. Обозначим через γ вероятность, что страховая компания не понесет убытков. Тогда вероятность, что количество страховых случаев будет не более, чем 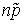, есть 
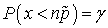. Используя нормальный закон распределения для случайной величины X, имеем:
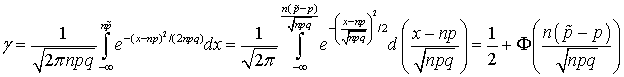.Здесь через Ф обозначена функция Лапласа, введенная в кванте 22. Из этого соотношения можно определить страховую ставку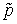 
. Зададим γ = 0,99 (вероятность, что страховая компания не разорится), вероятность наступления страхового случая p = 0,01 и число клиентов n = 1000. Из таблицы со значениями функции Лапласа
найдем, что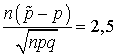 
. Отсюда находим 
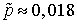.Аналогичная ситуация складывается и с инвестициями. Некоторые инвестиции могут дать весьма значительную прибыль, а какие-то окажутся убыточными. Основными целями инвестиционной компании являются максимизация прибыли и минимизация риска убытков. Поскольку заранее точно предсказать результат инвестиций невозможно, то единственно возможным путем оказываются статистические исследования.Пример 57.3Банк выдает кредиты 5 млн руб. под 10% сроком на 1 год. Риск невозврата кредита оценивается как 1%. Для уменьшения этого риска банк приобретает страховой полис на каждый кредит на S млн. руб., оплачивая страховой компании страховую премию в 2%. Оценить среднюю прибыль банка с одного кредита, если S=1, 3, 5 (страховой полис на 1 млн руб., 3 млн руб., 5 млн руб.).Рассмотрим случайную величину D = -0,02 S + X. Первое слагаемое определяет расходы банка на страховой полис, а второе — это случайная величина — сумма доходов и потерь банка, имеющая закон распределения:
0,5 млн руб. |
S - 5 млн руб. |
0,99 |
0,01 |
.Если приобретен страховой полис на 1 млн руб., то средняя прибыль составит:0,435 млн руб.,если приобретен страховой полис на 3 млн руб., то средняя прибыль составит:0,415 млн руб.,если приобретен страховой полис на 5 млн руб., то средняя прибыль составит:0,395 млн руб.Разумеется, приведенными здесь примерами не исчерпываются все возможности использования теории вероятности и математической статистики для решения задач экономического характера.Видеолекция «Использование методов математической статистики в экономике»: 
