29.
Биномиальное распределение
(см. квант 20):
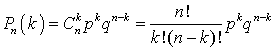. Введем в рассмотрение случайную величину X — количество удач при n испытаниях. Эта случайная величина может принимать целочисленные значения, от k = 0 до k = n. Формула Бернулли
, рассматриваемая как функция k, представляет собой закон распределения случайной величины и называется биномиальным распределением.Происхождение названия связано с формулой, называемой бином Ньютона:
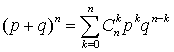(частные случаи этого выражения для n = 2 и n = 3 хорошо известны). Формула для биномиального распределения представляет собой k-й член суммы в биноме Ньютона. Изучим теперь свойства этого распределения.Легко видеть, что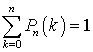 
. Действительно:
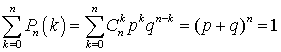. Здесь мы воспользовались биномом Ньютона и соотношением p + q = 1. Таким образом, формула для 
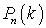на самом деле представляет собой закон распределения.Для вычисления математического ожидания и дисперсии количества удач в n испытаниях рассмотрим для начала вспомогательную случайную величину X1 — количество удач в одном испытании. Случайная величина X1 может принимать два значения 0 и 1 с вероятностями q и p, соответственно (это закон распределения случайной величины X1). Легко вычислить, что:
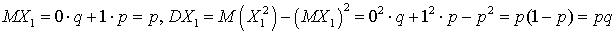. Далее случайную величину X можно рассматривать как сумму независимых случайных величин X1. Тогда на основании свойств математического ожидания и дисперсии от суммы случайных величин получаем:
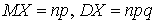. Выясним теперь поведение функции 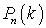при изменении k. Для этого запишем:
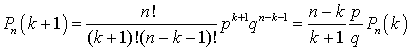и выясним, когда неотрицательный множитель 
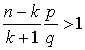(функция растет при переходе к следующему значению k), а когда 
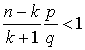(функция убывает при переходе к следующему значению). Решая неравенство 
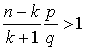можем получить 
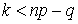. Это означает, что при значениях 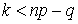функция 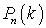растет, а при значениях 
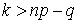, наоборот, убывает. Если 
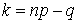(то есть рассматриваемый коэффициент равен единице), то это значение k и следующее за ним k + 1 дадут одинаковые значения функции 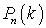, которые будут наиболее вероятными в распределении. Если np - q не целое число, то наибольшая вероятность будет достигаться при следующем целом значении k после np - q.Характерная зависимость биномиального распределения 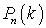от k представлена на рисунке ниже. Для построения графика было взято n = 10, p = 0,4.
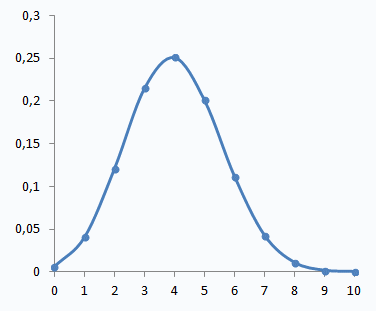Видеолекция «Биномиальное распределение»: 
