20.
Повторение испытаний. Формула Бернулли
, а второй — неудачей (разумеется, такое деление условно, и, возможно, кому-то захочется назвать два возможных исхода удачей и неудачей противоположным образом). Поставим задачу выяснить вероятность того, что за n испытаний произошло ровно k удач, неважно, в какой последовательности (естественно, что всегда 
).При заданной последовательности удач и неудач вероятность равна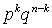 
(испытания независимы). Число различных способов, какими могут быть расположены k удач из n испытаний всего по формулам комбинаторики (см. квант 7) равно 
. По формуле для вероятности суммы несовместных событий для вероятности ровно k удач из n испытаний всего, получаем (формула Бернулли
):
. Рассмотрим несколько предельных случаев:Отметим, что при фиксированном n и при малых значениях k вероятность достаточно маленькая, и это обусловлено тем, что маловероятно, что нам не повезет ни разу (не будет ни одного удачного исхода). С ростом k эта вероятность будет расти, при некотором значении достигнет максимума и далее будет убывать, становясь при k близких к n снова достаточно малой. Малое значение вероятности при k, близких к n, обусловлено тем, что маловероятно, что все испытания будут удачные.Пример 20.1Кубик бросают 10 раз. Какова вероятность того, что 3 раза выпадет единица?Вероятность удачи (выпала единица) — p = 1/6, вероятность неудачи — q = 5/6. По формуле Бернулли:
, 
, 
. 
.Пример 20.2Тест состоит из 10-ти вопросов, по 4 варианта ответа на каждый вопрос. Один ответ верный, остальные — нет. Какова вероятность случайно ответить верно не менее чем на 1 вопрос, 2 вопроса, 3, 4, 5 ...?Вероятность удачи (верного ответа) — p = 0,25, вероятность неудачи — q = 0,75. По формуле Бернулли вычислим вероятности правильного ответа ровно на 1 вопрос, ровно на 2 вопроса и т.д.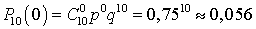
, 
, 
, 
, 
, 
, 
, 
, 
, 
,
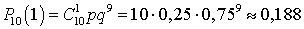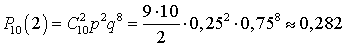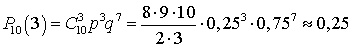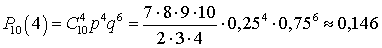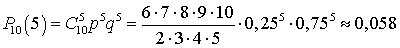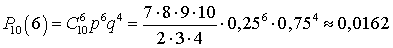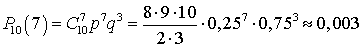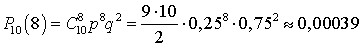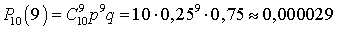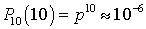.Так как события «ответить правильно ровно на 1 вопрос», «ответить правильно ровно на 2 вопроса» и так далее несовместны, находим:
, 
, 
, 
, 
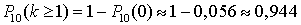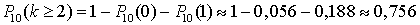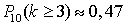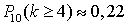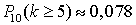. Видеолекция «Повторение испытаний. Формула Бернулли»: 
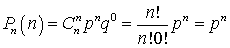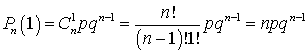