23.
Формула Пуассона
определялась формулой Бернулли
. При большом числе испытаний формула Бернулли
становится неудобной в использовании из-за больших значений факториала, и в кванте 21 была сформулирована приближенная формула (локальная теорема Лапласа). Формула Лапласа справедлива, когда вероятность удачи p не близка к нулю или единице. В реальном использовании формула Лапласа дает неплохое приближение, когда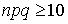 
. В случае, когда p мало (или q мало, так как можно переназвать удачу и неудачу) даже при большом числе испытаний n применение формулы Лапласа дает значительную погрешность. Для редких событий обычно используют другое приближение, а именно, считают, что n велико, а p — мало, так что их произведение — 
, где λ — некоторая константа. Для получения приближенной формулы воспользуемся формулой Бернулли, в которой перейдем к пределу при 
, так, чтобы величина оставалась постоянной:
.При вычислении предела мы воспользовались правилами вычисления предела от произведения и вторым замечательным пределом. Таким образом, мы получили, что при больших n и малых p вместо формулы Бернулли можно воспользоваться приближенной формулой:
, называемой формулой Пуассона, где 
. Пример 23.1Станок производит в день 10000 деталей. Вероятность того, что деталь окажется бракованной, составляет 0,0002. Найти вероятность того, что за день будет произведено ровно 5 бракованных деталей.Можно считать, что анализ каждой из 10000 деталей — это некоторое производимое испытание, причем все эти испытания независимы. В результате испытания возможны два исхода: удача с вероятностью 0,0002 (обнаружена бракованная деталь) и неудача с вероятностью 0,9998 (деталь качественная). Воспользуемся формулой Пуассона для вычисления того, что количество удач (найденных бракованных деталей) будет ровно 5:
, 
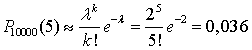. Примерно такой же результат дает и формула Бернулли, однако, расчеты по ней даже в этом простом примере оказываются существенно более громоздкими по сравнению с формулой Пуассона. Видеолекция «Формула Пуассона»: 
