Глоссарий
Бином Ньютона — 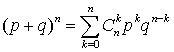.Биномиальное распределение — зависимость 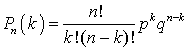.Варианта — значение объекта в совокупности.Вариационный ряд — варианты, записанные в возрастающей последовательности.Вероятностный смысл плотности распределения — 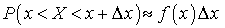.Вероятность попадания случайной величины в заданный интервал — 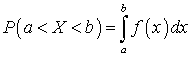.Вероятность появления хотя бы одного из независимых в совокупности событий — 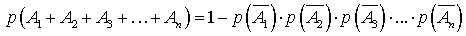.Вероятность появления хотя бы одного события — 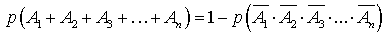.Вероятность произведения двух независимых событий — 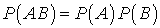.Вероятность произведения независимых в совокупности событий — 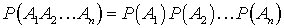.Вероятность произведения событий — 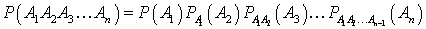.Вероятность суммы несовместных событий — 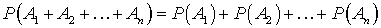.Вероятность суммы противоположных событий — 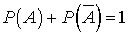.Вероятность того, что случайная величина Х примет значение в диапазоне (a, b) — 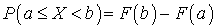.Взаимная корреляционная функция случайных функций X (t) и Y (t) — корреляционный момент случайных величин, соответствующих двум сечениям двух случайных функций при значениях аргумента t1 и t2, то есть 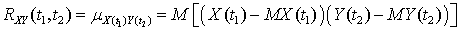.Выбор с возвращением — комбинации m элементов из n элементов, отличающиеся составом или порядком следования, причем выбранный элемент возвращается на место и может участвовать в дальнейшем выборе.Выборка бесповторная — способ осуществления выборки, когда отобранный объект впоследствии не возвращается в генеральную совокупность.Выборка повторная — способ осуществления выборки, когда отобранный объект впоследствии возвращается в генеральную совокупность и может участвовать в выборке повторно.Выборочная совокупность (выборка) — совокупность случайно отобранных объектов.Выборочный корреляционный момент двумерной случайной величины(X, Y) — 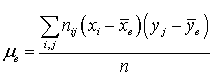.Выборочный коэффициент корреляции двумерной случайной величины (X, Y) — 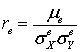.Вычисление дисперсии непрерывной случайной величины — 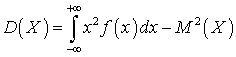.Генеральная совокупность — совокупность всех объектов, из которых производится выборка.Генератор случайных чисел — система на компьютере, выдающая случайные числа с равномерным распределением в диапазоне от нуля до единицы.Геометрическая вероятность — отношение меры множества l к мере множества L.Геометрическое распределение — закон распределения вида 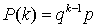.Гипергеометрическое распределение — закон распределения вида Eqn_gloss_018.gif.Гипотеза конкурирующая (альтернативная) — гипотеза, противоречащая нулевой.Гипотеза нулевая (основная) — гипотеза, выдвинутая для проверки.Гипотеза простая — гипотеза, состоящая из одного предположения.Гипотеза сложная — гипотеза, состоящая из нескольких простых.Гистограмма — способ графического представления статистического распределения с непрерывными значениями признака, для чего ось абсцисс разделяется на интервалы и на каждом интервале строится прямоугольник с высотой, равной числу вариант попавших в этот интервал (или доле этих вариант от объема выборки).Двумерная случайная величина — случайная величина, значение которой определяется двумя числами.Дисперсия случайной величины — 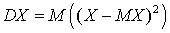.Дисперсионный анализ — анализ статистических данных, позволяющий установить воздействие фактора на значения случайной величины.Дисперсия «исправленная» выборочная — 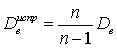.Дисперсия внутригрупповая — сумма групповых дисперсий, умноженных на объемы групп и деленную на объем всей совокупности: 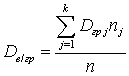.Дисперсия выборочная — среднее арифметическое квадратов отклонений значений признака в выборке от их выборочного среднего.Дисперсия генеральная — среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их генерального среднего.Дисперсия групповая (в j- группе) — среднее арифметическое квадратов отклонений значений признака, принадлежащих группе, от их группового среднего: 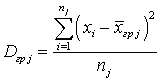.Дисперсия для нормального распределения 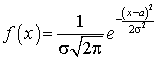 — 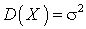.Дисперсия межгрупповая — сумма квадратов отклонений групповых средних от общего среднего, умноженных на объемы групп, и деленную на объем всей совокупности: 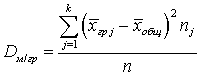.Дисперсия непрерывной случайной величины — 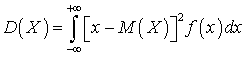.Дисперсия общая — среднее арифметическое квадратов отклонений значений признака, принадлежащих всей совокупности, от их общего среднего: 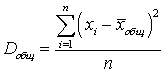.Дисперсия показательного распределения 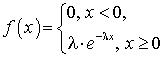 — 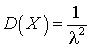.Дисперсия равномерно распределенной на (a, b) случайной величины — 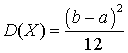.Дисперсия случайной функцииX (t) — функция DX (t), значение которой при каждом значении аргумента t есть дисперсия случайной величины — сечения X (t).Доверительный интервал — интервал, в который попадает значение оцениваемого параметра генеральной совокупности с заданной надежностью.Достоверное событие — событие, которое обязательно произойдет при любом испытании.Закон больших чисел — поведение суммы достаточно большого количества случайных величин становится почти закономерным.Закон распределения дискретной двумерной случайной величины — соответствие между ее возможными значениями (xi, yj) и вероятностями их реализации pij.Закон распределения дискретной случайной величины — соответствие между возможными значениями и их вероятностями.Интегральная теорема Лапласа — 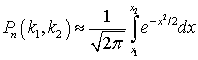, где 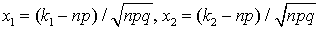.Интервальная оценка — оценка параметра генеральной совокупности интервалом значений, в который он попадает.Классическое определение вероятности — 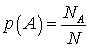.Количество комбинаций выбораm предметов изn с возвращением — nm.Количество перестановокn предметов — 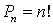.Количество размещенийm предметов изn — 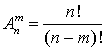.Количество сочетанийm предметов изn — 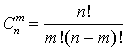.Комбинаторика — вычисление количество вариантов выбора m элементов из n элементов .Композиция — плотность распределения суммы независимых случайных величин.Коррелированные случайные величины — случайные величины, корреляционный момент которых не равен нулю.Коррелированные случайные функции — две случайные функции, если их взаимная корреляционная функция не равна тождественно нулю.Корреляционная функция случайной функцииX (t) — корреляционный момент случайных величин, соответствующих двум сечениям при значениях аргумента t1 и t2, то есть 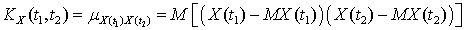.Корреляционный анализ — анализ статистических данных, позволяющий установить взаимосвязь случайных величин.Корреляционный момент — 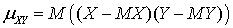.Коэффициент корреляции — 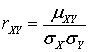.Критическая область — область значений статистического критерия, когда нулевая гипотеза отвергается.Критические точки — точки, разделяющие критическую область и область принятия гипотезы.Линейная регрессия — установление линейной зависимости между двумя случайными величинами 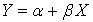. — 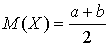.Математическое ожидание дискретной случайной величины — 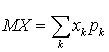.Математическое ожидание для нормального распределения 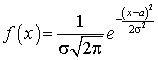 — 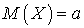.Математическое ожидание непрерывной случайной величины — 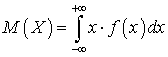.Математическое ожидание показательного распределения 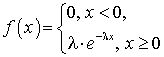 — 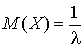.Математическое ожидание случайной функцииX (t) — функция MX (t), значение которой при каждом значении аргумента t есть математическое ожидание случайной величины — сечения X (t).Математическое ожидание функции одного случайного аргумента — 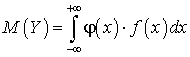.Метод Монте-Карло — метод, основанный на разыгрывании случайной величины, математическое ожидание которой равно вычисляемому значению.Наблюдаемое значение критерия — значение критерия (случайной величины), вычисленное по данным выборки (или выборок).Надежность (доверительная вероятность) — вероятность (близкая к единице), что значение оцениваемого параметра генеральной совокупности попадает в интервал.Нахождение функции распределения F (x) по плотности распределения f (x) — 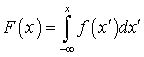.Невозможное событие — событие, которое не может произойти ни при каких испытаниях.Независимые в совокупности события — независимы каждые два из них и независимы каждое из них и все возможные произведения остальных.Независимые случайные величины — случайные величины, законы распределения которых не зависят от значений другой случайной величины.Независимые события — появление одного не сказывается на вероятности реализации другого события.Некоррелированные случайные величины — случайные величины, корреляционный момент которых равен нулю.Некоррелированные случайные функции — две случайные функции, если их взаимная корреляционная функция равна тождественно нулю.Неравенство Чебышева — 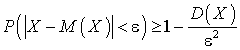.Несмещенная оценка — оценка параметра генеральной совокупности по выборке, когда математическое ожидание параметра выборки равно параметру генеральной совокупности.Несовместные события — события, в которых появление одного события исключает появление другого события.Нормальное распределение — 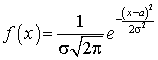.Нормированная взаимная корреляционная функция случайных функций X (t) и Y (t) — 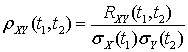.Нормированная корреляционная функция случайной функции X (t) — 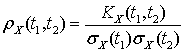.Нормированная нормально распределенная случайная величина — 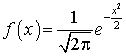.Область принятия гипотезы — область значений статистического критерия, когда нулевая гипотеза принимается.Общая сумма квадратов отклонений значений случайной величины от общего среднего — 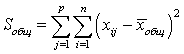.Объем совокупности — число объектов в этой совокупности.Остаточная сумма квадратов отклонений значений случайной величины от групповых средних — 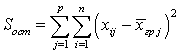.Отбор механический — отбор, при котором генеральная совокупность делится по порядку на столько групп, сколько объектов должно войти в выборку, и из каждой группы выбирается один объект.Отбор простой случайный — отбор, при котором объекты перемешивают и вытаскивают по одному наудачу.Отбор серийный — отбор, при котором генеральная совокупность делится на группы, и для исследования берется одна из групп.Отбор типический — отбор, при котором генеральная совокупность делится на отдельные части, и из каждой части наудачу отбирается некоторое количество объектов, при этом пропорции между количеством отобранных предметов каждой из частей определяются пропорциями объемов этих частей в генеральной совокупности.Ошибка второго рода — ошибка, когда принимается неправильная нулевая гипотеза.Ошибка первого рода — ошибка, когда отвергается правильная нулевая гипотеза.Перестановки — комбинации, составленные из одних и тех же элементов и отличающиеся порядком их следования.Плотность распределения 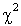с k степенями свободы — 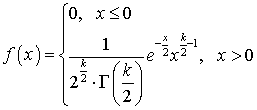.Плотность распределения суммы Z = X + Y двух случайных аргументов — 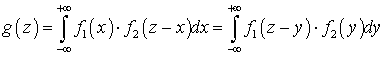.Плотность распределения вероятностей двумерной непрерывной случайной величины (X,Y) — 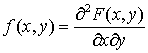.Плотность распределения вероятностей непрерывной случайной величины — 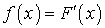.Плотность распределения Стьюдента с k степенями свободы — 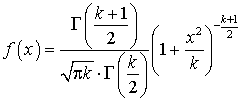.Плотность распределения Фишера—Снедекора  со степенями свободыk1 и k2 — 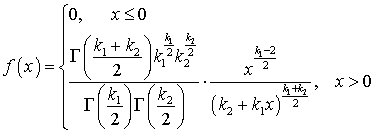.Плотность распределения функции одного случайного аргумента — 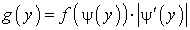.Показательное распределение — 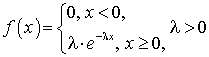.Полигон частот — набор точек (xi, ni) (или (xi, wi)), возможно соединенных ломаной линией, для представления статистического распределения выборки.Полная группа событий — в результате испытания обязательно реализуется хотя бы одно из события.Попарно несовместные события — каждая пара событий является несовместной.Произведение событий — событие, заключающееся в том, что произошли все из них.Пространство элементарных событий — множество всех элементарных событий.Противоположные события — два несовместных события, образующих полную группу событий.Равновероятные события — равновозможные события.Равновозможные события — при большом числе испытаний частота появления одинакова.Равномерное распределение — 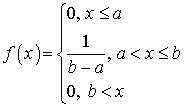.Размещения — комбинации, составленные выбором из n различных элементов m различных элементов, отличающиеся либо составом элементов, либо порядком их следования.Распределение «хи квадрат» — 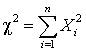, где 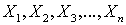 — нормально распределенные, нормированные, независимые случайные величины.Распределение Стьюдента — 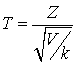, где Z — нормально распределенная нормированная случайная величина, V — независимая от Z случайная величина, которая распределена по закону 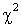с k степенями свободы.Распределение Фишера—Снедекора — 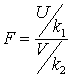, где U и V — независимые случайные величины, распределенные по закону 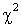со степенями свободы k1 и k2.Свойства функции плотности распределения непрерывной случайной величины — 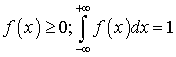.Сечение случайной функции — случайная функция, взятая при некотором значении аргумента.Случайная величина — величина, которая в результате испытания будет принимать одно и только одно значение, заранее неизвестное и зависящее от случайных причин.Случайная величина дискретная — случайная величина, которая принимает отдельные, изолированные возможные значения.Случайная величина непрерывная — случайная величина, которая принимает любые значения из некоторого промежутка.Случайная функция — функция неслучайного аргумента, которая при каждом значении аргумента является случайной величиной.Случайное событие — событие, которое может произойти, а может не произойти.Смещенная оценка — оценка параметра генеральной совокупности по выборке, когда математическое ожидание параметра выборки не равно параметру генеральной совокупности.Совместные события — события, в которых появление одного события не исключает появление другого события.Сочетания — комбинации, составленные выбором m различных элементов из n различных элементов, отличающиеся только составом (но не порядком следования).Среднее арифметическое случайной величины — 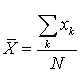.Среднее выборочное — среднее арифметическое значений признака в выборке.Среднее генеральное — среднее арифметическое значений признака в генеральной совокупности.Среднее групповое — среднее арифметическое значений признака, принадлежащих группе.Среднее общее — среднее арифметическое значений признака, принадлежащих всей совокупности.Среднеквадратичное отклонение — квадратный корень из дисперсии.Статистическая гипотеза — гипотеза о виде неизвестного распределения или о параметрах известного распределения.Статистический критерий — выбранная случайная величина, которая служит для проверки нулевой гипотезы.Статистическое определение вероятности — относительная частота появления события в совокупности.Статистическое распределение выборки — совокупность вариант и соответствующих им частот (или относительных частот).Сумма событий — событие, заключающееся в том, что произошло хотя бы одно из них.Теорема Бернулли — теорема, устанавливающая связь между вероятностью события и относительной частотой его появления.Теорема сложения вероятностей несовместных событий — 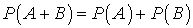.Теорема сложения вероятностей совместных событий — 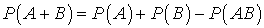.Теорема Чебышева — 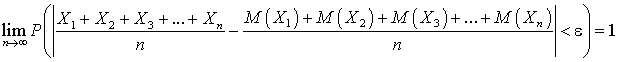.Теоретическая функция распределения — функция распределения генеральной совокупности.Точечная оценка — оценка параметра генеральной совокупности по выборке одним числом.Уровень значимости — вероятность совершить ошибку первого рода.Условная вероятность 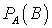 — вероятность наступления события, вычисленная в предположении, что некоторое другое событие (условие) наступило.Факторная сумма квадратов отклонений групповых средних от общего среднего — 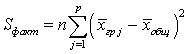.Формула Бернулли — 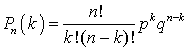.Формула Лапласа (локальная предельная теорема Лапласа) — 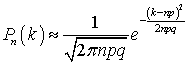.Формула полной вероятности — 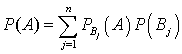.Формула Пуассона — 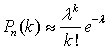, где 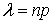.Формулы Байеса — 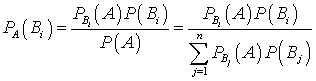.Функция двух случайных аргументов — 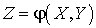.Функция Лапласа — 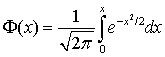.Функция одного случайного аргумента — 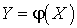.Функция распределения вероятностей непрерывной случайной величины — 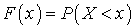.Функция распределения двумерной случайной величины (X, Y) — функция двух вещественных чисел F(x, y) = P(X < x, Y < y), означающая, что вероятность того что случайная величина X примет значение меньше x, а случайная величина Y примет значение меньше y.Функция распределения для нормально распределенной случайной величины — 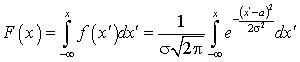.Функция распределения показательного распределения — 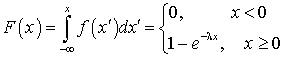.Функция распределения равномерно распределенной случайной величины — 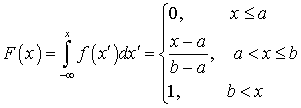.Центральная предельная теорема — теорема, устанавливающая, что распределение суммы большого числа взаимно независимых случайных величин близко к нормальному.Частота — количество данной варианты в совокупности.Частота относительная — отношение количества данной варианты в совокупности к объему совокупности.Элементарное событие — событие, которое не разделимо на более простые.Эмпирическая функция распределения (функция распределения выборки) — функция 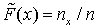, где nx — число вариант со значением меньше x.
В начало