55.
Основы корреляционного анализа
Пусть имеется совокупность двух случайных величин (X, Y), значения которой извлекаются из двумерной генеральной совокупности, распределенной нормально. Предположение о нормальном распределении вполне оправдано в силу центральной предельной теоремы. Требуется определить, коррелируют ли между собой случайные величины X и Y. Если генеральная совокупность имеет большой объем, то заключение о корреляции двух случайных величин делают по выборке. 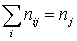Результатом выборки является корреляционная таблица, определяющая соответствие между парой значений случайных величин (xi, yj) и относительной частотой появления этой комбинации в выборке nij, при этом: — объем выборки; — относительная частота появления yj; 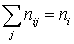— относительная частота появления xi.Определение. Выборочным корреляционным моментом двумерной случайной величины (X, Y) называется 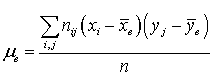.Определение. Выборочным коэффициентом корреляции двумерной случайной величины (X, Y) называется 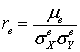.Замечание. Удобство введения выборочного коэффициента корреляции наряду с корреляционным моментом связано с тем, что коэффициент корреляции — величина безразмерная, и не зависит от выбора системы единиц измерения X и Y.Теорема. Выборочный корреляционный момент может быть посчитан как: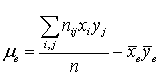.Доказательство. Аналогично соответствующей теореме в кванте 45.Пусть сделана выборка объема n и вычислен выборочный коэффициент корреляции 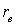. Разумеется, выборочный коэффициент корреляции 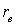вовсе не равен генеральному коэффициенту корреляции 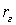, а представляет всего лишь его оценку. Таким образом, ставится статистическая задача: проверить нулевую гипотезу 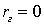(гипотеза о равенстве нулю генерального коэффициента корреляции). При этом альтернативная (конкурирующая) гипотеза: 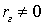. Для проверки гипотезы задается некоторый уровень значимости α. В качестве критерия для проверки нулевой гипотезы выбирают случайную величину: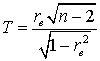.Случайная величина T при справедливости нулевой гипотезы имеет распределение Стьюдента с k = n - 2 степенями свободы. Далее по таблице критических точек распределения Стьюдента (см. ниже), по заданному уровню значимости α и числу степеней свободы k = n - 2 определяют критические точки tкр. Этих критических точек — две, они отличаются знаком, поскольку коэффициент корреляции 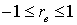, и отличие от нуля может быть как в сторону положительных значений, так и в сторону отрицательных. Если по данным выборки наблюдаемое значение случайной величины 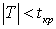, то нулевую гипотезу принимают (или, более точно, нет оснований ее отвергнуть). Если по данным выборки наблюдаемое значение случайной величины 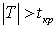, то нулевую гипотезу отвергают, а принимают конкурирующую гипотезу.

Таблица критических точек распределения Стьюдента

Степени свободы k

Уровень значимости α (2-сторонняя критическая область)

0,1

0,05

0,02

0,01

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞

6,31
2,92
2,35
2,13
2,01
1,94
1,89
1,86
1,83
1,81
1,80
1,78
1,77
1,76
1,75
1,75
1,74
1,73
1,73
1,73
1,72
1,72
1,71
1 , 71
1 , 71
1 , 71
1 , 71
1,70
1,70
1,70
1,68
1,67
1,66
1,64

12,7
4,30
3,18
2,78
2,57
2,45
2,36
2,3!
2,26
2.23
2,20
2,18
2,16
2,14
2,13
2,12
2,11
2,10
2,09
2,09
2,08
2,07
2,07
2,06
2,06
2,06
2,05
2,05
2,05
2,04
2,02
2,00
1,98
1,96

31,82
6,97
4,54
3,75
3,37
3,14
3,00
2,90
2,82
2,76
2,72
2,68
2,65
2,62
2,60
2,58
2,57
2,55
2,54
2,53
2,52
2,51
2,50
2,49
2,49
2,48
2,47
2,46
2,46
2,46
2,42
2,39
2,36
2,33

63,7
9,92
5,84
4,60
4,03
3,71
3,50
3,36
3,25
3,17
3,11
3,05
3,01
2,98
2,95
2,92
2,90
2,88
2,86
2,85
2,83
2,82
2,81
2,80
2,79
2,78
2,77
2,76
2,76
2,75
2,70
2,66
2,62
2,58

 

0,05

0,025

0,01

0,005

Уровень значимости α (1-сторонняя критическая область)
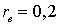Пример 55.1По выборке объема n = 62, извлеченной из нормальной двумерной генеральной совокупности определен выборочный коэффициент корреляции: . При уровне значимости 0,05 проверить гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе 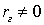.Наблюдаемое значение критерия равно: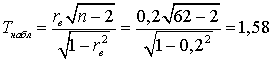.Как уже упоминалось выше, при конкурирующей гипотезе 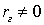критическая область — двусторонняя. При заданных 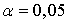и 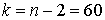находим: 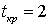. Поскольку 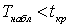, то оснований отвергнуть гипотезу нет, и она принимается.Видеолекция «Основы корреляционного анализа»:
Перейти к выполнению теста: Основы корреляционного анализа. Тест
В начало