51.
Групповая, внутригрупповая, межгрупповая и общая дисперсия
и общим средним. Введем теперь аналогичные понятия для дисперсий.Определение. Групповой дисперсией (в j группе) называют среднее арифметическое квадратов отклонений значений признака, принадлежащих группе, от их группового среднего: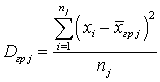 
.Определение. Внутригрупповой дисперсией называют сумму групповых дисперсий, умноженных на объемы групп и деленную на объем всей совокупности: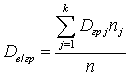
.Определение. Межгрупповой дисперсией называют сумму квадратов отклонений групповых средних от общего среднего, умноженных на объемы групп и деленную на объем всей совокупности: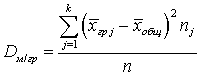
.Определение. Общей дисперсией называют среднее арифметическое квадратов отклонений значений признака, принадлежащих всей совокупности, от их общего среднего: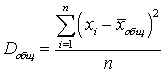
.Пример 51.1Даны две группы объектов: (0, 1, 1, 1, 2) и (1, 2, 2, 3). Найти групповые и общее средние, групповые, внутригрупповую, межгрупповую и общую дисперсии.Групповое среднее для первой группы:
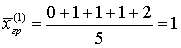.Групповое среднее для второй группы:
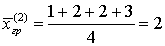.Общее среднее:
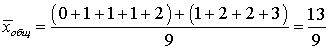.Легко видеть, что общее среднее можно рассчитать как сумму групповых средних, умноженных на число объектов в группе, и полученную сумму разделить на число объектов в совокупности.Групповая дисперсия для первой группы:
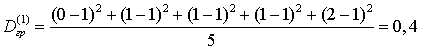.Групповая дисперсия для второй группы:
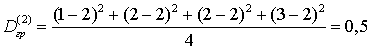.Внутригрупповая дисперсия:
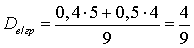.Межгрупповая дисперсия:
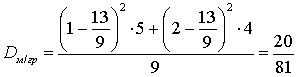.Общая дисперсия:
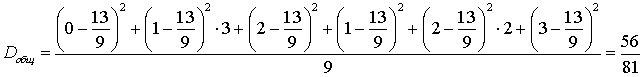.Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий 
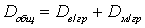.Доказательство.Для уменьшения выкладок рассмотрим частный случай, когда совокупность разделена на две группы. Элементы первой группы будем обозначать символом x(1), а элементы второй группы — x(2). Общая дисперсия есть:
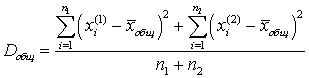.Внутригрупповая дисперсия есть:
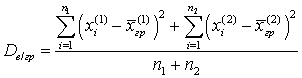.Межгрупповая дисперсия есть:
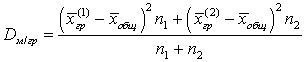.Вычислим:
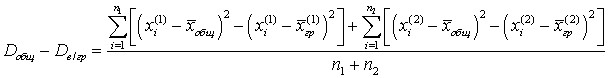.Применяя формулу для разности квадратов к первой сумме, получим:
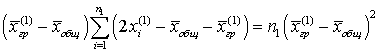.Аналогичное выражение будет и для второй суммы. В итоге имеем:
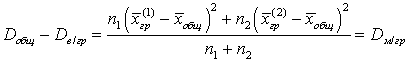.Теорема доказана.Видеолекция «Групповая, внутригрупповая, межгрупповая и общая дисперсия»: 
