46.
Линейная регрессия
 , то выбирая вместо Y другую величину
, то выбирая вместо Y другую величину 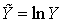 , получим линейную связь
, получим линейную связь  . Поэтому будем в дальнейшем рассматривать линейную связь случайных величин X и Y и будем говорить о так называемой линейной регрессии
. Поэтому будем в дальнейшем рассматривать линейную связь случайных величин X и Y и будем говорить о так называемой линейной регрессии Yна X. Другими словами, будем строить функцию, связывающую две случайных величины, X и Y, в виде
Yна X. Другими словами, будем строить функцию, связывающую две случайных величины, X и Y, в виде  , где коэффициенты α и β определяются таким образом, чтобы функция
, где коэффициенты α и β определяются таким образом, чтобы функция 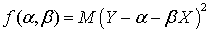 имела наименьшее возможное значение (среднеквадратичная линейная регрессия).Теорема. Линейная среднеквадратичная регрессия
имела наименьшее возможное значение (среднеквадратичная линейная регрессия).Теорема. Линейная среднеквадратичная регрессия случайной величины Yна случайную величину Xимеет вид
случайной величины Yна случайную величину Xимеет вид  , где
, где  .Доказательство.Преобразуем функцию
.Доказательство.Преобразуем функцию 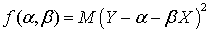 к виду:
к виду: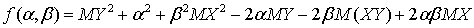 и исследуем ее на экстремум, для чего вычислим производные:
и исследуем ее на экстремум, для чего вычислим производные: ,
,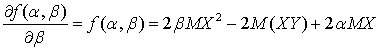 .Экстремум определяется равенством нулю частных производные, таким образом, имеем систему:
.Экстремум определяется равенством нулю частных производные, таким образом, имеем систему: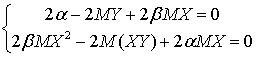 .Домножая первое уравнение на и вычитая его из второго, получим коэффициент:
.Домножая первое уравнение на и вычитая его из второго, получим коэффициент: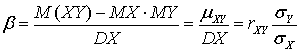 .Выражая α из первого уравнения и подставляя найденное значение β, получим:
.Выражая α из первого уравнения и подставляя найденное значение β, получим: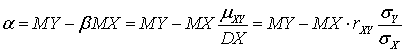 .То, что эти значения дают именно минимум f (α, β) (а не максимум), очевидно из того факта, что максимума здесь быть не может. Это на примере можно охарактеризовать тем, что прямую, в принципе, можно провести сколь угодно далеко от экспериментальных точек. Теорема доказана.Пример 46.1Для совокупности двух случайных величин X и Y, заданных законом распределения (см. таблицу ниже), построить прямую, осуществляющую линейную среднеквадратичную регрессию Y на X.
.То, что эти значения дают именно минимум f (α, β) (а не максимум), очевидно из того факта, что максимума здесь быть не может. Это на примере можно охарактеризовать тем, что прямую, в принципе, можно провести сколь угодно далеко от экспериментальных точек. Теорема доказана.Пример 46.1Для совокупности двух случайных величин X и Y, заданных законом распределения (см. таблицу ниже), построить прямую, осуществляющую линейную среднеквадратичную регрессию Y на X.
|
x1 = -1 |
x2 = 0 |
x3 = 1 |
y1 = 0 |
0,1 |
0,2 |
0,1 |
y2 = 2 |
0,3 |
0,2 |
0,1 |
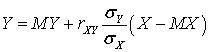 . Вычислим все величины, входящие в уравнение:
. Вычислим все величины, входящие в уравнение: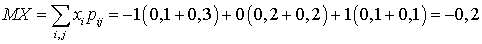 ,
,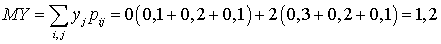 ,
,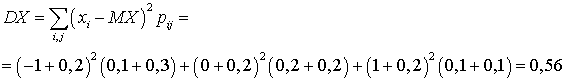 ,
,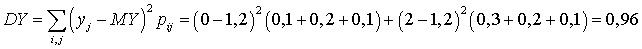
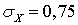
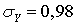
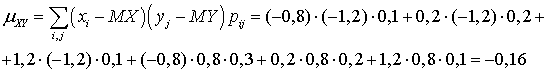
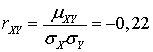 .В итоге закон регрессии Y на X имеет вид:
.В итоге закон регрессии Y на X имеет вид: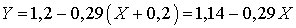 .Видеолекция «Линейная регрессия»:
.Видеолекция «Линейная регрессия»: 

