Теория вероятностей и математическая статистика: Распределение двух случайных величин

44.

Распределение двух случайных величин

До настоящего момента мы рассматривали случайные величины, которые определялись только одним значением, так называемые одномерные случайные величины

. Можно говорить также о двумерной, трехмерной и т.д. случайных величинах. Мы остановимся на рассмотрении двумерных случайных величин, случай многомерных случайных величин рассматривается аналогично.Определение. Двумерной случайной величиной

называется случайная величина, значение которой определяется двумя числами, то есть двумерную случайную величину можно рассматривать как совокупность случайных величин (X, Y). Далее вводятся понятия, относящиеся к двумерным случайным величинам, по аналогии, как это было сделано в случае одномерных случайных величин.Пример 44.1Подбрасывают два кубика. Двумерной случайной величиной будет случайная величина, в которой первое значение есть число очков, выпавших на первом кубике, а второе значение — число очков на втором кубике.Пример 44.2Имеется совокупность одинаковых деталей. Несмотря на то, что детали названы одинаковыми, длина и ширина каждой из них имеют различные значения в пределах погрешности их изготовления. Соответственно, двумерной случайной величиной в этом случае будет совокупность двух значений — длины и ширины детали.Различают дискретные

и непрерывные двумерные случайные величины

, в зависимости от того, какие значения могут принимать ее значения. Первый из рассмотренных выше примеров есть дискретная случайная величина, а второй — непрерывная.Определение. Законом распределения дискретной двумерной случайной величины

называется соответствие между ее возможными значениями (x_i, y_j) и вероятностями их реализации p_ij.Способы задания:

аналитический (в виде формулы);
табличный.

Возможен также графический способ (в трехмерной системе координат), однако он не обладает такой же наглядностью, как это было в случае одномерной случайной величины. Задать закон распределения в виде таблицы можно следующим способом:

	x₁	x₂	…	x_n
y₁	p₁₁	p₂₁	…	p_n1
y₂	p₁₂	p₂₂	…	p_n2
…	…	…	…	…
y_m	p_1m	p_2m	…	p_nm

Очевидно, что сумма всех вероятностей, находящихся в таблице, ввиду не совместности событий, образующих полную группу, равна единице. Сумма вероятностей, находящихся в i-м столбце есть сумма вероятностей по всем возможным значениям Y и представляет собой вероятность того, что случайная величина X примет значение x_i. И, аналогично, сумма вероятностей, находящихся в j-й строке, есть сумма вероятностей по всем возможным значениям X и представляет собой вероятность того, что случайная величина Y примет значение y_j. Соответственно, просуммировав значения в каждом столбце, мы получим закон распределения случайной величины X, просуммировав значения в каждой строке, получим закон распределения случайной величины Y.Определение. Функцией распределения двумерной случайной величины (X, Y)

называют функцию двух вещественных чисел F(x, y) = P(X < x, Y < y), означающую, что вероятность того что случайная величина X примет значение меньше x, а случайная величина Y примет значение меньше y.Это определение подходит как для непрерывных, так и для дискретных двумерных случайных величин.Свойства функции распределения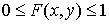

.Свойство следует из аналогичных свойств вероятности.
F(x, y) — неубывающая функция по каждому аргументу.Свойство следует из того, что при x1 < x2 событие X < x2 полностью включает в себя и событие X < x1 , а, значит, 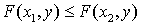. Аналогично можно показать это и для значения y.
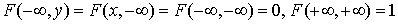.Действительно, в первой цепочке равенств каждая из функций есть вероятность невозможного события, а в последнем равенстве функция распределения есть вероятность достоверного события.
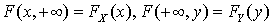, то есть эти предельные значения определяют функцию распределения случайной величины X и случайной величины Y соответственно.Так как событие 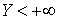— это достоверное событие, то 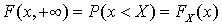и, аналогично, — для второго равенства.
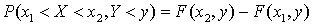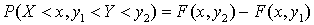,.Можно получить из аналогичных свойств для вероятностей.
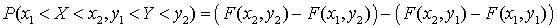.Получается применением свойства 5 к обеим переменным.

Определение. Плотностью распределения вероятностей двумерной непрерывной случайной величины (X, Y)

называют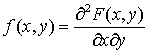

.Из определения сразу следует, что найти функцию распределение двумерной непрерывной случайной величины, зная плотность распределения, можно, вычислив интеграл:

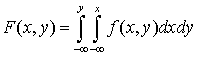.Свойства плотности вероятности

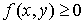.Свойство следует из того, что F (x,y) — неубывающая функция по каждому аргументу.
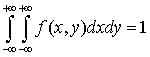.Действительно, написанный интеграл равен функции распределения .
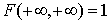Плотности вероятности каждой из составляющих двумерной непрерывной случайной величины равны: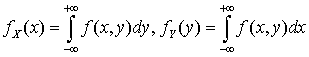.Продифференцировав по x 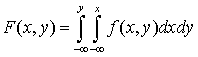и взяв 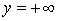получим: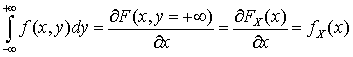.Аналогично можно получить и второе равенство.

Видеолекция «Распределение двух случайных величин»:

Перейти к выполнению теста: Распределение двух случайных величин. Тест