41.
Распределения «хи квадрат», Стьюдента, Фишера—Снедекора
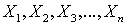— нормально распределенные, независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а дисперсия — единице. То есть закон распределения каждой из них имеет вид:
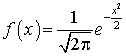.Тогда сумма квадратов этих случайных величин:
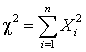распределена по закону 
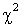с k = n степенями свободы. Если случайные величины связаны линейным соотношением 
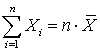, то число степеней свободы равно k= n - 1.Плотность распределения 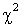с k = n степенями свободы имеет вид:
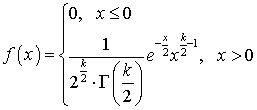,где 
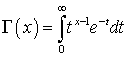. В частности, 
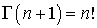.Видно, что распределение 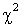определяется всего одним параметром — числом степеней свободы k. С увеличением числа степеней свободы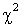 
медленно приближается к нормальному распределению.Пусть Z — нормально распределенная случайная величина с математическим ожиданием равным нулю и дисперсией равной единице. Пусть V — независимая от Z случайная величина, которая распределена по закону 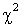с k степенями свободы. Тогда величина
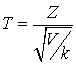имеет распределение, называемое t-распределением, или распределением Стьюдента
с k степенями свободы.Плотность распределения Стьюдента имеет вид: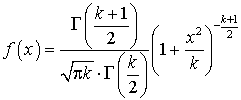
.С ростом числа степеней свободы распределение Стьюдента быстро приближается к нормальному распределению.Пусть U и V — независимые случайные величины, распределенные по закону 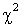со степенями свободы k1 и k2. Тогда величина
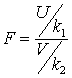имеет распределение, которое называется распределением Фишера—Снедекора со степенями свободы k1 и k2.Плотность распределения Фишера—Снедекора со степенями свободы k1 и k2 имеет вид: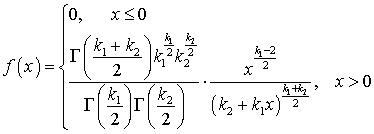
. Видеолекция «Распределения «хи квадрат», Стьюдента, Фишера—Снедекора»: 
