40.
Функция двух случайных аргументов и ее распределение
 , определялась функция нескольких, например, двух аргументов. Аналогично можно ввести понятие функции двух случайных аргументов.Определение. Если каждой паре возможных значений случайных величин X и Y ставится в соответствие одно возможное значение случайной величины Z, то это означает, что Z является функцией двух случайных аргументов
, определялась функция нескольких, например, двух аргументов. Аналогично можно ввести понятие функции двух случайных аргументов.Определение. Если каждой паре возможных значений случайных величин X и Y ставится в соответствие одно возможное значение случайной величины Z, то это означает, что Z является функцией двух случайных аргументов X и Y.
X и Y.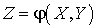 Покажем, как найти распределение Z, если распределения X и Y нам известны.
Покажем, как найти распределение Z, если распределения X и Y нам известны.- Пусть аргумент X и Y — дискретные независимые случайные величины.Если различным значениям аргументов X и Yсоответствуют различные значения функции
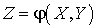 , а законы их распределений имеют вид:
, а законы их распределений имеют вид:
X
x1
x2
x3
x4
…
xn
P
p1(x)
p2(x)
p3(x)
p4(x)
…
pn(x)
В этом случае закон распределения функцииY
y1
y2
y3
y4
…
ym
P
p1(y)
p2(y)
p3(y)
p4(y)
…
pm(y)
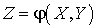 будет:
Если среди значений
будет:
Если среди значенийZ
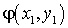
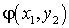
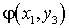
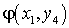
…
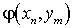
P
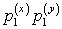
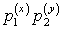
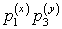
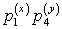
…
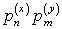
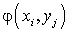 есть равные между собой, то следует складывать вероятности повторяющихся значений Z, как это делается в случае функции одного случайного аргумента.Пример 40.1Имеются 2 случайные величины X и Y, распределенные следующим образом:
есть равные между собой, то следует складывать вероятности повторяющихся значений Z, как это делается в случае функции одного случайного аргумента.Пример 40.1Имеются 2 случайные величины X и Y, распределенные следующим образом:
X
1
2
P
0,3
0,7
Определить распределение случайной величиныY
2
3
P
0,4
0,6
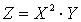 .Решение. Возможные значения Z есть произведение каждого возможного значенияX на каждое возможное значение Y:
.Решение. Возможные значения Z есть произведение каждого возможного значенияX на каждое возможное значение Y: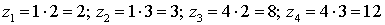 .Вероятности вычисляются умножением соответствующих вероятностей. В результате получим закон распределения:
.Вероятности вычисляются умножением соответствующих вероятностей. В результате получим закон распределения:
Z
2
3
8
12
P
0,12
0,18
0,28
0,42
- Пусть X и Y — непрерывные случайные величины с плотностями распределения
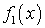 и
и 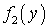 . Доказано, что если X и Y — независимы, то плотность распределения
. Доказано, что если X и Y — независимы, то плотность распределения 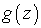 суммы
суммы 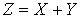 определяется равенством:
определяется равенством: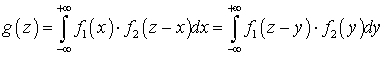 .Если возможные значения аргументов неотрицательны, то
.Если возможные значения аргументов неотрицательны, то 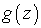 определяется формулой:
определяется формулой: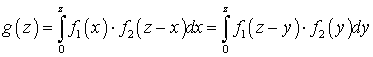 .
.
 .Закон распределения вероятностей называется устойчивым
.Закон распределения вероятностей называется устойчивым , если композиция из таких законов дает тот же самый закон. Например, нормальный закон распределения устойчив. Если X и Y распределены нормально с математическими ожиданиями a1 и a2 и дисперсиями D1 и D2, то композиция этих величин также распределена нормально, причем ее математическое ожидание и дисперсия есть a1 + a2 и D1 + D2.Пример 40.2Имеются 2 случайные величины X и Y, распределенные следующим образом:
, если композиция из таких законов дает тот же самый закон. Например, нормальный закон распределения устойчив. Если X и Y распределены нормально с математическими ожиданиями a1 и a2 и дисперсиями D1 и D2, то композиция этих величин также распределена нормально, причем ее математическое ожидание и дисперсия есть a1 + a2 и D1 + D2.Пример 40.2Имеются 2 случайные величины X и Y, распределенные следующим образом: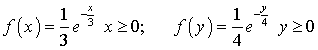 .Найти плотность распределения (композицию)
.Найти плотность распределения (композицию) 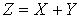 .Решение.
.Решение.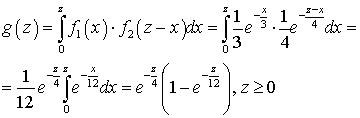 . Видеолекция «Функция двух случайных аргументов и ее распределение»:
. Видеолекция «Функция двух случайных аргументов и ее распределение»: 

