39.
Функция одного случайного аргумента и ее распределение
По аналогии с тем, как в курсе математического анализа определялась функция, можно ввести понятие функции случайного аргумента.Определение. Если каждому возможному значению случайной величины X ставится в соответствие одно возможное значение Y, то это означает, что Y является функцией случайного аргумента X.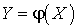Покажем, как найти распределение Y, если распределение X нам известно.
  1. Пусть аргумент X — дискретная случайная величина.Если различным значениям аргумента Xсоответствуют различные значения функции 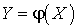, то вероятности соответствующих значений X и Y равны. То есть законы распределения имеют вид :

    X

    x1

    x2

    x3

    x4

    …

    xn

    P

    p1

    p2

    p3

    p4

    …

    pn

    Y

    φ(x1)

    φ(x2)

    φ(x3)

    φ(x4)

    …

    φ(xn)

    P

    p1

    p2

    p3

    p4

    …

    pn
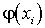    При этом нижние строки в таблицах совпадают.Если среди значений есть равные между собой, то следует складывать вероятности повторяющихся значений Y. Например, если в приведенной выше таблице 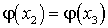, то таблица примет вид:

    Y

    φ (x1)

    φ (x2)

    φ (x4)

    …

    φ (xn)

    P

    p1

    p2 + p3

    p4

    …

    pn
  2. Пусть аргумент X — непрерывная случайная величина с плотностью распределения f (x). Если 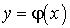 — дифференцируемая, монотонно возрастающая (убывающая) функция, обратная функция к которой есть 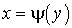, то плотность распределения g (y) случайной величины Y есть: .
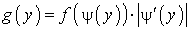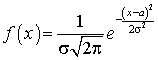Пример 39.1Имеется нормально распределенная случайная величина с плотностью распределения, равной . Найти распределение функции 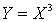.Решение.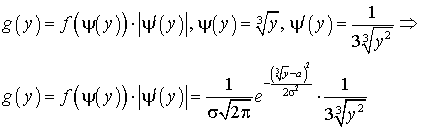,Пример 39.2Имеется нормально распределенная случайная величина с плотностью распределения равной 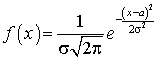. Найти распределение функции 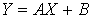.Решение.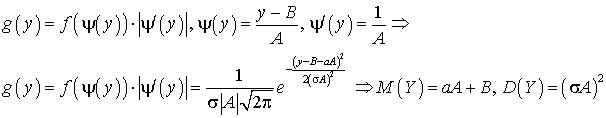Математическое ожидание функции одного случайного аргумента
  1. Пусть X — дискретная случайная величина, 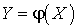. В соответствии с законом распределения:

    Y

    φ (x1)

    φ(x2)

    φ(x3)

    φ(x4)

    …

    φ(xn)

    P

    p1

    p2

    p3

    p4

    …

    pn
  2. Пусть X — непрерывная случайная величина. 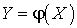.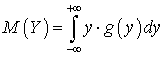Можно показать, что
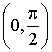Пример 39.3Плотность распределения непрерывной случайной величины X есть f (x) =sin x в интервале и 0 вне этого интервала. Найти математическое ожидание функции 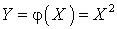.Решение. . Интегрируя по частям, получим 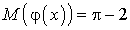. Видеолекция «Функция одного случайного аргумента и ее распределение»:
Перейти к выполнению теста: Функция одного случайного аргумента и ее распределение. Тест
В начало