32.
Плотность распределения вероятностей непрерывной случайной величины
непрерывной случайной величины называют функцию:
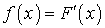. Из определения следует, что F (x) — первообразная к f (x). Первообразная определяется с точностью до константы, а она задается условием 
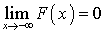.Замечание 1. Для дискретной случайной величины F (x) можно построить, а f (x) — нет.Теорема. Вероятность попадания случайной величины в заданный интервал есть 
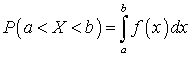.Доказательство. По свойству функции F (x) можно написать, что 
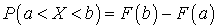. Используя основную теорему интегрального исчисления (формулу Ньютона
—Лейбница), получим: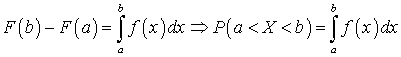
.Геометрический смысл — площадь под кривой графика функции f (x).
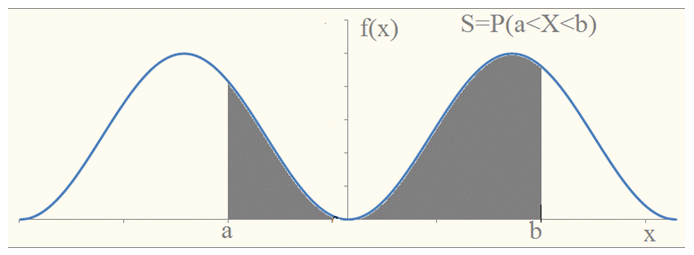Пример 32.1Вычислить 
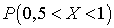, если плотность распределения вероятностей имеет вид:
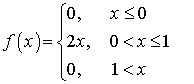Решение. 
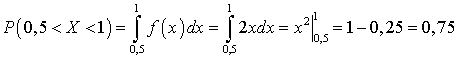.Пример 32.2Вычислить 
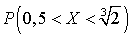, если плотность распределения вероятностей имеет вид:
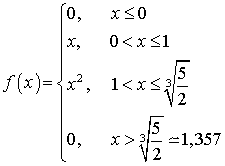Решение. .
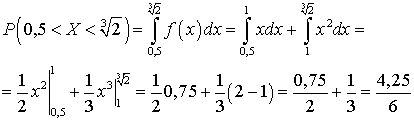Свойства функции плотности распределенияНахождение F (x) по f (x): 
. 
. 
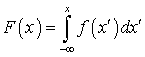. Пример 32.3Найти F (x), если плотность распределения имеет вид:
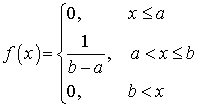. Решение.
. 
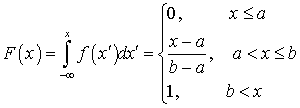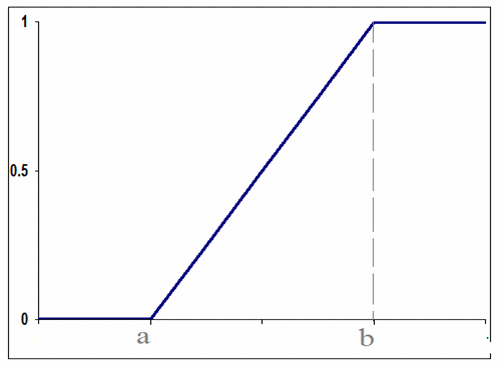Вероятностный смысл плотности распределения
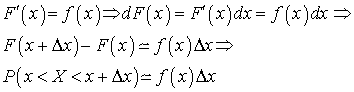. Видеолекция «Плотность распределения вероятностей непрерывной случайной величины»: 
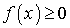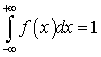