30.
Геометрическое и гипергеометрическое распределения
. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность . Этот закон распределения и называется геометрическим распределением
. Название происходит из того, что величина представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать: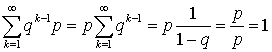
, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:
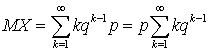. Для вычисления суммы воспользуемся следующим приемом — заменим 
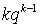на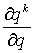 
и вынесем производную за знак суммы, в итоге получим:
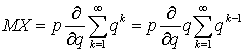. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна 
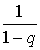. Вычисляя производную, запишем:
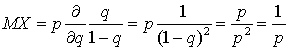. Аналогично можно получить выражение для 
:
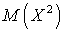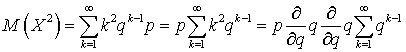. Заменяя сумму на ее значение 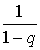, вычисляем:
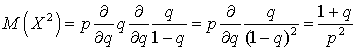. Таким образом, имеем выражение для дисперсии:
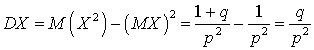. Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).Пример 30.1Вероятность попадания в мишень из винтовки равна 0,8. Найти математическое ожидание и дисперсию случайной величины — количества выстрелов до первого попадания.Математическое ожидание 
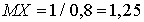, дисперсия 
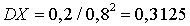. Полученные результаты означают, что при вероятности попадания 0,8 попадание будет в среднем с 1—2 выстрела.Гипергеометрическое распределениеПусть имеется N предметов, из них M — помеченных. Наудачу вытаскивают n предметов. Какова вероятность, что среди вытащенных n предметов будет m помеченных? Разумеется 
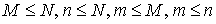. Для решения задачи посчитаем общее число элементарных исходов, каким можно вытащить n предметов из N, и число благоприятных исходов, то есть когда среди n вытащенных предметов окажется m помеченных. Согласно формулам комбинаторики (см. квант 7) общее число элементарных исходов есть 
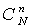. Составить комбинацию m помеченных предметов, когда всего их M, можно 
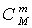способами. При этом на каждый способ составить комбинацию m помеченных предметов из M есть 
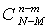способов взять оставшиеся n - m предметов из N - Mне помеченных. Таким образом, число благоприятных элементарных исходов есть 
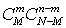. Согласно классическому определению вероятности получаем ответ к задаче:
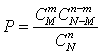. Если значения N, M и n заданы, то полученная вероятность, рассматриваемая как функция m, представляет собой закон распределения случайной величины — числа помеченных предметов m в выборке n. Этот закон распределения называется гипергеометрическим распределением.Пример 30.2В ящике 6 синих и 4 красных шара. Вытаскиваем 5 шаров. Найти вероятность того, что среди них окажется 3 синих.По формуле гипергеометрического распределения имеем: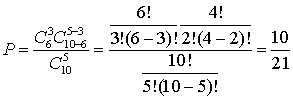
. Видеолекция «Геометрическое и гипергеометрическое распределение»: 
