18.
Формула полной вероятности и формулы Байеса
, обычно называемых гипотезами
. Пусть некоторое событие A может наступить при условии появления одного из этих событий с известными условными вероятностями: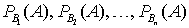 
. Возникает вопрос, как посчитать безусловную вероятность события A. Ответ дает следующая теорема.Теорема (формула полной вероятности). Пусть — полная группа несовместных событий (гипотезы). Если известны условные вероятности 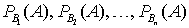, то безусловную вероятность наступления события A можно посчитать по формуле:
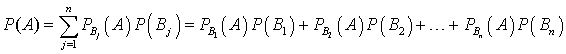. Без доказательства.Пример 18.1Вам надо купить определенную книгу. Всего имеем 3 магазина. Вероятность того, что книга будет куплена в первом магазине, составляет 50%, во втором — 30%, в третьем — 20%. В первом магазине 40% книг «пиратского» издания, во втором — 50% «пиратских» книг и в третьем — 20%. Какова вероятность, что купленная вами книга окажется «пиратской»?Обозначим через 
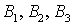— события, заключающиеся в том, что мы попали в первый, второй и третий магазины, соответственно, а событие A — то, что купленная книга — «пиратская». По условию 
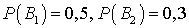и 
. События 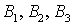— несовместны, и образуют полную группу. Из условия известно также, что 
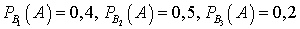. Используя формулу полной вероятности, найдем, что вероятность купить «пиратскую» книгу (неважно, в каком магазине) равна:
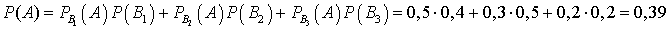Теорема (формулы Байеса
). Пусть A может наступить при условии появления одного из несовместных событий , образующих полную группу. Допустим, что произведено испытание, в результате которого произошло событие A. Тогда вероятность того, что реализовалась гипотеза Bi, если известно, что событие A произошло, может быть вычислена по формулам: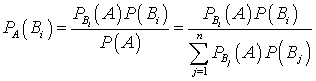
. Доказательство. По теореме умножения вероятностей:
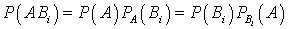. Выражая 
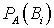, найдем:
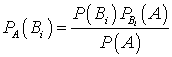. Знаменатель можно представить, используя формулу полной вероятности. Теорема доказана.Пример 18.2Вам надо купить определенную книгу. Всего имеем 3 магазина. Вероятность того, что книга будет куплена в первом магазине равна 50%, во втором — 30%, в третьем — 20%. В первом магазине имеется 40% книг «пиратского» издания, во втором — 50% «пиратских» книг и в третьем — 20%. Вы купили книгу в каком то из трех магазинов, и она оказалась «пиратской». Какова вероятность того, что книга куплена в первом магазине, втором, третьем?Условие задачи совпадает с предыдущей. Сохраняя прежние обозначения и используя полученные результаты, применим формулы Байеса: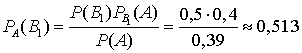
, 
, 
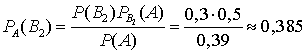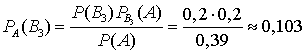. Видеолекция «Формула полной вероятности и формулы Байеса»: 
