10.
Сложение вероятностей несовместных событий. Противоположные события
A + B двух событий A и B называют событие, состоящее в появлении хотя бы одного из этих событий.Аналогично определяется сумма трех, четырех и более событий.Суммой 
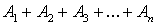называют событие, состоящее в появлении хотя бы одного из этих событий.Пример 10.1Группа из 25 студентов идет на зачет. События 
состоят в том, что первый студент сдаст зачет, второй студент сдаст зачет, третий студент сдаст зачет, и т.д. Сумма этих событий есть событие, заключающееся в том, что хотя бы один из них зачет сдаст.Определение. События называются попарно несовместными, если любые два из этих событий несовместны.Теорема. Вероятность появления хотя бы одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий: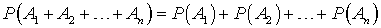
.Доказательство. Следует из третьей аксиомы.Теорема. Сумма вероятностей попарно несовместных событий 
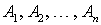, образующих полную группу, равна единице, то есть:
. Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то: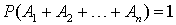
. По предыдущей теореме:
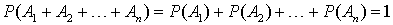. Теорема доказана.Определение. Противоположными событиями называют два несовместных события, образующих полную группу.Обозначают противоположные события чертой сверху: событие Ā противоположно событию A.Пример 10.2Студент идет на зачет. События, что он сдаст зачет и что он его не сдаст, являются противоположными. Действительно, это 2 события, они несовместны и образуют полную группу событий.Пример 10.3Студент идет на экзамен. События, что он сдаст экзамен на 5 и что он его сдаст на 2, противоположными не являются, поскольку они не образуют полную группу событий (возможны еще оценки 3 и 4).Пример 10.4Студент идет на экзамен. События, что он сдаст экзамен на 5, на 4, на 3, на 2 противоположными не являются, поскольку это не 2, а 4 события.Теорема. Сумма вероятностей противоположных событий равна единице, то есть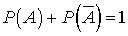 
. Доказательство. Следует из определения противоположных событий и предыдущей теоремы.Пример 10.5В рассмотренной в 9 кванте задаче про дни рождения группа состоит из 30 студентов. Пусть событие A заключается в том, что все дни рождения различны. Тогда событие Ā означает, что есть повторяющиеся дни рождения. Как найдено выше 
, . Согласно только что доказанной теореме — 
, то есть вероятность того, что будут одинаковые дни рождения хотя бы у двух студентов 
. Видеолекция «Сложение вероятностей несовместных событий. Противоположные события»: 
