4.
Аксиомы теории вероятностей
.- Каждому событию A поставлено в соответствие некоторое число
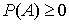, называемое вероятностью этого события. - Вероятность достоверного события равна единице:
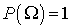. - Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.
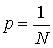. Убедимся в справедливости данного утверждения. Пусть все элементарные события равновозможны (равновероятны), а общее число элементарных событий равно . По второй аксиоме вероятность появления ходя бы одного из элементарных событий равна 1, или 
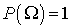. Поскольку все элементарные события попарно несовместны, то из третьей аксиомы следует, что 
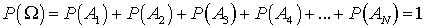. Поскольку по условию элементарные события равновозможны, то 
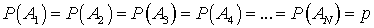, следовательно получаем, что 
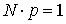, или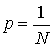 
.Равновероятные элементарные события, как правило, возникают при механических испытаниях (подбрасывание игральной кости, подбрасывание монеты, вытягивание карты из колоды).Замечание. Формула 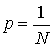справедлива только в том случае, когда пространство элементарных событий конечно, а сами элементарные события равновероятны.Пример 4.1Подбрасывается игральная кость. Какова вероятность, что выпадет шестерка?Пространство элементарных событий состоит из 6 равновероятных событий (1, 2, 3, 4, 5, 6). Следовательно, 
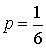. Пример 4.2Подбрасываются 2 монеты. Какова вероятность, что на обеих выпадет орел?Пространство элементарных событий состоит из 4 равновероятных событий (орел — орел, орел — решка, решка — орел, решка — решка). Следовательно, 
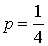. Следствие 2. В случае, если пространство элементарных событий состоит из Nравновозможных элементарных событий, то вероятность события A равна 
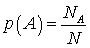, где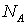 
— количество элементарных событий, благоприятствующих наступлению события A.Пример 4.3Подбрасывается игральная кость. Какова вероятность, что выпадет число, меньшее 5?Пространство элементарных событий состоит из 6 равновероятных событий (1, 2, 3, 4, 5, 6). Нас устраивают 4 из них (1, 2, 3, 4). Следовательно, 
. Пример 4.4Подбрасываются 2 игральные кости. Какова вероятность, что сумма выпавших очков больше 10?Пространство элементарных событий состоит из 36 равновероятных событий (6 ∙ 6). Нас устраивают 3 из них (6 + 6, 6 + 5, 5 + 6). Следовательно, . Видеолекция «Аксиомы теории вероятностей»: 
