2.
Классическое и статистическое определение вероятностей
. Когда мы хотим дать количественную оценку возможности реализации какого либо события, мы разлагаем все события, которые могут произойти на элементарные события (см. квант 1). Например, если речь идет о вытаскивании карты из колоды, содержащей 36 карт, то под элементарными событиями понимается возможность извлечь шестерку пик, семерку пик и т.д. Общее количество элементарных событий в данном примере будет равно 36, ровно столько, сколько карт в колоде. В случае, когда мысленно проводятся механические испытания (вытаскивание карт из колоды, подбрасывание монеты и т.д.), естественно предположить, что все элементарные события равновозможны, т.е. нет преимуществ в реализации одних элементарных событий перед другими. Тогда количественной оценкой возможности реализации события А будет являться классическое определение вероятности данного события. Определяется эта вероятность как отношение числа элементарных событий, благоприятствующих наступлению события А к общему количеству элементарных событий: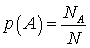
.Пример 2.1В рассмотренном примере с картами если мы зададимся вопросом, какова вероятность, что вынутая из колоды наугад карта окажется достоинством не ниже десятки, то по данной формуле это легко вычислить. Действительно, поскольку 
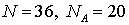(4 туза, 4 короля и т.д.), то 
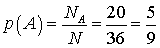.Пример 2.2Бросается игральная кость. Какова вероятность, что выпадет шестерка?Количество элементарных событий равно 6. Только одно из них благоприятствует наступлению события А. Следовательно, вероятность, что выпадет шестерка, равна 
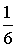. Статистическое определение вероятности. Часто оказывается довольно сложно представить результат испытания в виде совокупности элементарных событий. Кроме того, не всегда элементарные события равновероятны. Например, когда студент идет на экзамен, четыре элементарных события — оценка 2, 3, 4, 5 — равновероятными не являются. В подобных случаях наряду с классическим используют статистическое определение вероятности. В качестве статистической вероятности события принимается относительная частота его реализации при большом числе испытаний. Если проводится n испытаний и при этом событие А реализовалось m раз, то относительная частота появления события А есть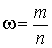 
.Например, если монета подбрасывалась 2000 раз, и орел при этом выпал 982 раза, то статистическая вероятность события, что выпадет орел, равна относительной частоте его появления 
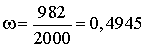. Недостатком статистического определения вероятности является его неоднозначность. Так, например, если мы повторно проведем серию из 2000 подбрасываний монеты, и в этой серии орел выпадет не 982, а 1028 раз, то статистическая вероятность в новой серии испытаний окажется равной 
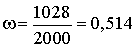. Заметим, что классическое определение вероятности есть некоторая идеализация статистической вероятности. Действительно, если сравнить классическую и статистическую вероятность выпадения шестерки на игральной кости, то классическая вероятность равна 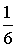, в то время, как статистическая, являющаяся результатом большого числа испытаний не будет в точности равна 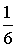из-за того, что идеальных кубических фигур в природе не существует, а, следовательно, будет отличие от 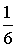. Видеолекция «Классическое и статистическое определение вероятностей»: 
